已知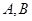 为椭圆
为椭圆 上两动点,
上两动点,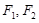 分别为其左右焦点,直线
分别为其左右焦点,直线 过点
过点 ,且不垂直于
,且不垂直于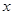 轴,
轴, 的周长为
的周长为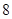 ,且椭圆的短轴长为
,且椭圆的短轴长为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知点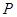 为椭圆
为椭圆 的左端点,连接
的左端点,连接 并延长交直线
并延长交直线 于点
于点 .求证:直线
.求证:直线 过定点.
过定点.
已知幂函数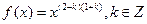 ,且
,且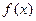 在
在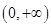 上单调递增.
上单调递增.
(Ⅰ)求实数 的值,并写出相应的函数
的值,并写出相应的函数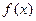 的解析式;
的解析式;
(II)若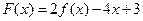 在区间
在区间 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(III)试判断是否存在正数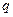 ,使函数
,使函数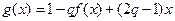 在区间
在区间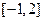 上的值域为
上的值域为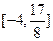 . 若存在,求出
. 若存在,求出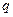 的值;若不存在,请说明理由
的值;若不存在,请说明理由
已知函数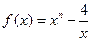 ,且
,且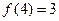 .
.
(Ⅰ)判断 的奇偶性并说明理由;
的奇偶性并说明理由;
(Ⅱ)判断 在区间
在区间 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(Ⅲ)若在区间 上,不等式
上,不等式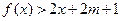 恒成立,试确定实数
恒成立,试确定实数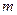 的取值范围.
的取值范围.
若集合 ,
,
(Ⅰ)若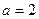 ,求集合
,求集合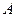 ;
;
(Ⅱ)若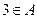 ,求实数
,求实数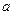 的取值范围.
的取值范围.
计算: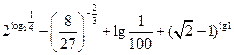
(Ⅱ)已知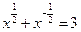 ,求
,求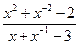 的值.
的值.
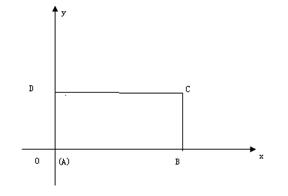
在平面直角坐标系中,已知矩形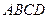 的长为2,宽为1,
的长为2,宽为1,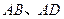 边分别在x轴、y轴的正半轴上,
边分别在x轴、y轴的正半轴上,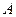 点与坐标原点重合(如图4所示),将矩形折叠,使
点与坐标原点重合(如图4所示),将矩形折叠,使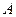 点落在线段
点落在线段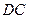 上.
上.
(Ⅰ)若折痕所在直线的斜率为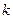 ,试写出折痕所在直线的方程;
,试写出折痕所在直线的方程;
(Ⅱ)设折痕线段为EF,记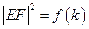 ,求
,求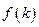 的解析式.
的解析式.