已知数列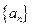 的前n项和为
的前n项和为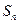 ,且
,且
(1)求数列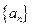 的通项;
的通项;
(2)若数列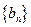 中,
中,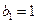 ,点P(
,点P(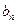 ,
,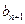 )在直线
)在直线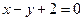 上,记
上,记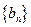 的前n项和为
的前n项和为 ,当
,当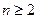 时,试比较
时,试比较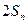 与
与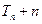 的大小
的大小
在数列 中,已知
中,已知
(1)证明数列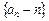 是等比数列
是等比数列
(2)  为数列
为数列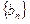 的前
的前 项和,求
项和,求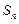 的表达式
的表达式
(14分)已知椭圆C的中心在坐标原点,焦点在x轴上,离心率 .直线
.直线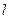 :
: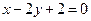 与椭圆C相交于
与椭圆C相交于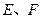 两点, 且
两点, 且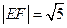
(1)求椭圆C的方程
(2)点P(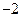 ,0),A、B为椭圆C上的动点,当
,0),A、B为椭圆C上的动点,当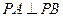 时,求证:直线AB恒过一个定点.并求出该定点的坐标.
时,求证:直线AB恒过一个定点.并求出该定点的坐标.
(13分)已知函数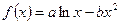 图象上一点P(2,
图象上一点P(2, )处的切线方程为
)处的切线方程为
(1)求 的值(2)若方程
的值(2)若方程 在
在 内有两个不等实根,求
内有两个不等实根,求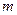 的取值范围(其中
的取值范围(其中 为自然对数的底)
为自然对数的底)
(12分)如图,在棱长为2的正方体ABCD -A1B1C1D1中,E、F分别为A1D1和CC1 的中点.
(1)求证:EF∥平面ACD1
(2)求三棱锥E-ACD1的体积与正方体ABCD -A1B1C1D1的体积之比