如图,已知长方形 的两条对角线的交点为
的两条对角线的交点为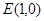 ,且
,且 与
与 所在的直线方程分别为
所在的直线方程分别为 .
.
(1)求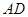 所在的直线方程;
所在的直线方程;
(2)求出长方形 的外接圆的方程.
的外接圆的方程.
(本小题满分10分)
已知圆 和圆
和圆 的极坐标方程分别为
的极坐标方程分别为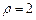 ,
,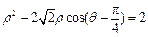 .
.
(1)把圆 和圆
和圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
(本小题满分12分)已知函数f (x) = ax2 + 2ln(1-x),其中a∈R.
(1)是否存在实数a,使得f (x)在x = 处取极值?若存在,求出a的值,若不存在,说明理由;
处取极值?若存在,求出a的值,若不存在,说明理由;
(2)若f (x)在[-1,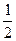 ]上是减函数,求实数a的取值范围.
]上是减函数,求实数a的取值范围.
(本小题满分12分)
某厂工人在2010年里,如果有1个季度完成生产任务,则得奖金300元;如果有2个季度完成生产任务,则可得奖金750元;如果有3个季度完成生产任务,则可得奖金1260元;如果有4个季度完成生产任务,可得奖金1800元;如果工人四个季度都未完成任务,则没有奖金,假设某工人每季度完成任务与否是等可能的,求他在2010年一年里所得奖金的分布列及其数学期望。
(本小题满分12分)设随机变量X的概率分布为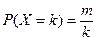 (k=1,2,3,4):
(k=1,2,3,4):
(Ⅰ)确定常数 的值;
的值;
(Ⅱ)写出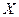 的分布列;
的分布列;
(Ⅲ)计算 的值.
的值.
(本小题满分12分)已知函数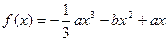 在
在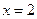 时取得极值.
时取得极值.
(1)求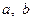 满足的关系式;(2)当
满足的关系式;(2)当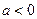 时,求函数
时,求函数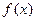 的单调递增区间.
的单调递增区间.