已知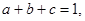
(1)求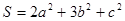 的最小值及取最小值时
的最小值及取最小值时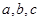 的值。
的值。
(2)若 ,求
,求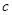 的取值范围。
的取值范围。
(本小题满分14分)已知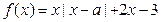 (Ⅰ)当
(Ⅰ)当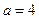 ,
,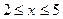 时,问
时,问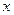 分别取何值时,函数
分别取何值时,函数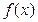 取得最大值和最小值,并求出相应的最大值和最小值;(Ⅱ)若
取得最大值和最小值,并求出相应的最大值和最小值;(Ⅱ)若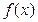 在R上恒为增函数,试求
在R上恒为增函数,试求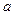 的取值范围;
的取值范围;
(Ⅲ)已知常数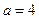 ,数列
,数列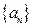 满足
满足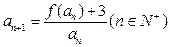 ,试探求
,试探求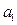 的值,使得数列
的值,使得数列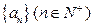 成等差数列.
成等差数列.
(本小题满分12分)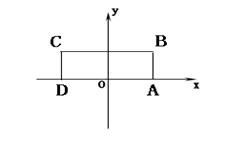
如图,在矩形ABCD中,已知A(2,0)、C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足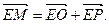 (Ⅰ)求点M的轨迹方程;
(Ⅰ)求点M的轨迹方程;
(Ⅱ)已知点F(0,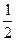 ),过点F的直线l与点M的轨迹相交于Q、R两点,且
),过点F的直线l与点M的轨迹相交于Q、R两点,且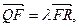 求实数
求实数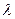 的取值范围.
的取值范围.
(本小题满分12分)2009年4月22日是第40个“世界地球日” (World Earth Day),在某校举办的《2009“世界地球日”》知识竞赛中,甲、乙、丙三人同时回答一道有关保护地球知识的问题,已知甲回答对这道题的概率是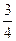 ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是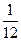 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是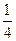 .
.
(Ⅰ)求乙、丙两人各自回答对这道题的概率.
(Ⅱ)求甲、乙、丙三人中恰有两人回答对该题的概率.
(本小题满分12分)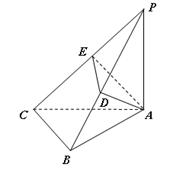 (如图),
(如图),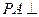 平面
平面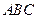 ,
,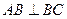 .
.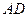 垂直于
垂直于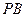 于
于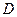 ,
,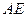 垂直于
垂直于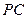 于
于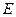 .
.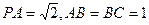 .
.
(Ⅰ) 求证: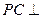 平面
平面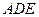 ;
;
(Ⅱ) 求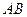 与平面
与平面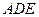 所成的角;
所成的角;
(Ⅲ)求平面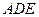 与平面
与平面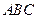 所成的二面角的大小.
所成的二面角的大小.
|
(本小题满分12分)在锐角△ABC中,角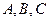 的对边分别为
的对边分别为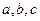 ,且满足
,且满足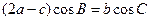 . (Ⅰ)求角B的大小; (Ⅱ)设
. (Ⅰ)求角B的大小; (Ⅱ)设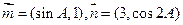 ,试求
,试求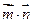 的取值范围.
的取值范围.