如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD= BC. 点E、F分别是棱PB、边CD的中点.
BC. 点E、F分别是棱PB、边CD的中点.
(1)求证:AB⊥面PAD;
(2)求证:EF∥面PAD.
(本小题满分12分)如图,在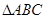 中,点
中,点 在
在 边上,
边上,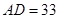 ,
, ,
,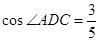 .
.
(1)求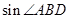 的值;
的值;
(2)求 的长.
的长.
已知函数
 ,
,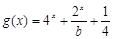 ,且
,且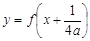 为偶函数.设集合
为偶函数.设集合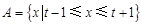 .
.
(Ⅰ)若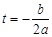 ,记
,记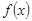 在
在 上的最大值与最小值分别为
上的最大值与最小值分别为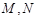 ,求
,求 ;
;
(Ⅱ)若对任意的实数 ,总存在
,总存在
 ,使得
,使得 对
对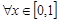 恒成立,试求
恒成立,试求 的最小
的最小
值.
已知抛物线
 ,准线与
,准线与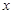 轴的交点为
轴的交点为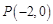 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)如图,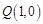 ,过点
,过点 的直线
的直线 与抛物线
与抛物线 交于不同的两点
交于不同的两点 ,AQ与BQ分别与抛物线
,AQ与BQ分别与抛物线 交于点
交于点
C,D,设AB,DC的斜率分别为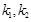 ,
,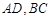 的斜率分别为
的斜率分别为 ,问:是否存在常数
,问:是否存在常数 ,使得
,使得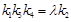 ,
,
若存在,求出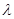 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知各项均为正数的数列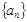 的前
的前 项和为
项和为 ,且
,且 . 在数列
. 在数列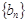 中,
中,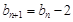 ,
, .
.
(Ⅰ)求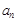 ,
,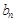 ;
;
(Ⅱ)设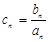 求数列
求数列 的前项和
的前项和 .
.
如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点, .
.
(Ⅰ)求证:直线EA⊥平面PAB;
(Ⅱ)求直线AE与平面PCD所成角的正切值.