设函数f (x)的定义域为M,具有性质P:对任意x∈M,都有f (x)+f (x+2)≤2f (x+1).
(1)若M为实数集R,是否存在函数f (x)=ax (a>0且a≠1,x∈R) 具有性质P,并说明理由;
(2)若M为自然数集N,并满足对任意x∈M,都有f (x)∈N. 记d(x)=f (x+1)-f (x).
(ⅰ) 求证:对任意x∈M,都有d(x+1)≤d(x)且d(x)≥0;
(ⅱ) 求证:存在整数0≤c≤d(1)及无穷多个正整数n,满足d(n)=c.
设 ,
, ,Q=
,Q= ;若将
;若将 ,
, ,
, 适当排序后可构成公差为1的等差数列
适当排序后可构成公差为1的等差数列 的前三项
的前三项 (I)在使得
(I)在使得 ,
, ,
, 有意义的条件下,试比较
有意义的条件下,试比较 的大小;
的大小;
(II)求 的值及数列
的值及数列 的通项;
的通项;
(III)记函数 的图象在
的图象在 轴上截得的线段长为
轴上截得的线段长为 ,设
,设 ,求
,求 .
.
设函数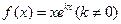
(1)求曲线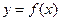 在点
在点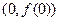 处的切线方程;
处的切线方程;
(2)求函数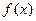 的单调区间;
的单调区间;
(3)若函数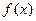 在区间
在区间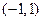 内单调递增,求
内单调递增,求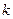 的取值范围.
的取值范围.
已知函数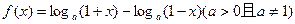
(1)讨论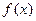 的奇偶性与单调性;
的奇偶性与单调性;
(2)若不等式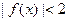 的解集为
的解集为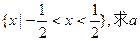 的值;
的值;
(3)(文)设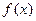 的反函数为
的反函数为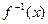 ,若关于
,若关于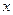 的不等式
的不等式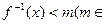 R)有解,求
R)有解,求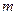 的取值范围.
的取值范围.
(理)设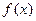 的反函数为
的反函数为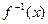 ,若
,若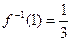 ,解关于
,解关于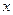 的不等式
的不等式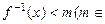 R).
R).
已知曲线C: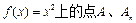 的横坐标分别为1和
的横坐标分别为1和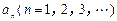 ,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且
,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且 ).设区间
).设区间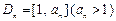 ,当
,当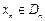 时,曲线C上存在点
时,曲线C上存在点 使得xn的值与直线AAn的斜率之半相等.
使得xn的值与直线AAn的斜率之半相等.
(1)证明: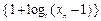 是等比数列;
是等比数列;
(2)当

 对一切
对一切 恒成立时,求t的取值范围;
恒成立时,求t的取值范围;
(3)记数列{an}的前n项和为Sn,当 时,试比较Sn与n + 7的大小,并证明你的结论.
时,试比较Sn与n + 7的大小,并证明你的结论.
已知函数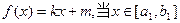 时,
时,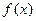 的值域为
的值域为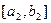 ,当
,当
时,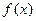 的值域为
的值域为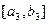 ,依次类推,一般地,当
,依次类推,一般地,当 时,
时,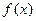 的值域为
的值域为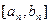 ,其中k、m为常数,且
,其中k、m为常数,且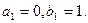
(1)若k=1,求数列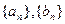 的通项公式;
的通项公式;
(2)项m=2,问是否存在常数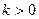 ,使得数列
,使得数列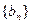 满足
满足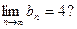 若存在,求k的值;若不存在,请说明理由;
若存在,求k的值;若不存在,请说明理由;
(3)若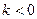 ,设数列
,设数列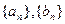 的前n项和分别为Sn,Tn,求
的前n项和分别为Sn,Tn,求 。
。