已知公差不为0的等差数列{an}的首项a1=2,且 ,
, ,
, 成等比数列.
成等比数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1+2b2+22b3+…+2n-1bn=an,求数列{nbn}的前n项和Tn..
(本小题满分16分)已知数列{an}满足a1=0,a2=2,且对任意m、n∈N*都有
(1)求a3,a5;
(2)设 (n∈N*),证明:数列{bn}是等差数列;
(n∈N*),证明:数列{bn}是等差数列;
(3)设cn=
 qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.
qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.
(本小题满分16分)已知函数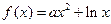
(1)当 时,求函数
时,求函数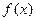 在
在 的值域
的值域
(2)求函数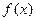 的单调区间
的单调区间
(3)若函数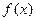 在区间
在区间 上不单调,求实数
上不单调,求实数 的取值范围
的取值范围
(本小题满分16分)为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本 (元)与月处理量
(元)与月处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该单位不亏损?
(本小题满分14分)已知函数 .
.
(1)求 的单调递增区间; (2)求
的单调递增区间; (2)求 在区间
在区间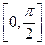 上的最值及相应的x值.
上的最值及相应的x值.
(3)将函数 的图象向左平移
的图象向左平移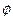
 个单位后,所得的函数恰好是偶函数,求
个单位后,所得的函数恰好是偶函数,求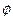 的最小值。
的最小值。
(本小题满分14分)
已知集合A为不等式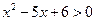 的解集,B=
的解集,B=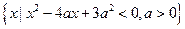 ,
,
(1)求解集合A;(2)若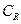 A
A B,求
B,求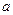 的取值范围;
的取值范围;
(3)若 ,求
,求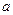 的取值范围
的取值范围