(本小题满分15分)
在等比数列{an}中,首项为 ,公比为
,公比为 ,
,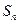 表示其前n项和.
表示其前n项和.
(I)记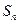 =A,
=A,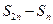 = B,
= B,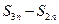 = C,证明A,B,C成等比数列;
= C,证明A,B,C成等比数列;
(II)若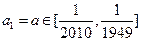 ,
,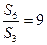 ,记数列
,记数列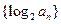 的前n项和为
的前n项和为 ,当n取何值时,
,当n取何值时, 有最小值.
有最小值.
(本小题满分14分)
已知二次函数 为偶函数,函数
为偶函数,函数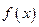 的图象与直线y=x相切.[]
的图象与直线y=x相切.[]
(I)求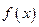 的解析式
的解析式
(II)若函数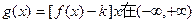 上是单调减函数,求k的取值范围;
上是单调减函数,求k的取值范围;
(本小题满分14分)
已知0是坐标原点,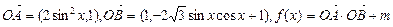 ,
,
(I)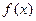 的单调递增区间;
的单调递增区间;
(II)若f(x)的定义域为 ,值域为[2,5],求m的
,值域为[2,5],求m的 值。
值。
本小题满分14分) 在△ABC中,角A,B,C所对的边分别为a,b,c,
在△ABC中,角A,B,C所对的边分别为a,b,c,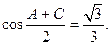
(I)求 的值;
的值;
(II)若 的值.
的值.
、(本小题满分16分)
已知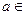 R,函数
R,函数
 R,
R, 为自然对数的底数)。
为自然对数的底数)。
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)若函数 在
在 上单调递增,求
上单调递增,求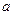 的取值范围;
的取值范围;
(3)函数 是否为R上的单调函数,若是,求出
是否为R上的单调函数,若是,求出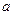 的取值范围;若不是,请说明理由。
的取值范围;若不是,请说明理由。