已知 是
是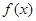 的导函数,
的导函数,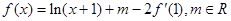 ,且函数
,且函数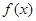 的图象过点
的图象过点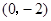 .
.
(1)求函数 的表达式;
的表达式;
(2)求函数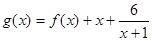 的单调区间和极值.
的单调区间和极值.
(本小题满分14分)已知函数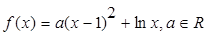 .
.
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2) 时,令
时,令 ,求
,求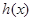 在
在 的最大值和最小值;
的最大值和最小值;
(3)当 时,函数
时,函数 图像上的点都在不等式组
图像上的点都在不等式组 所表示的区域内,求实数a的取值范围.
所表示的区域内,求实数a的取值范围.
(本小题满分13分)一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为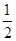 ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为X,求X的分布列和数学期望E(X).
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(本小题满分12分)如图所示,一根水平放置的长方体枕木的安全负荷与它的厚度d的平方和宽度a的乘积成正比,同时与它的长度 的平方成反比.
的平方成反比.
(1)在a>d>0的条件下,将此枕木翻转90°(即宽度变为了厚度),枕木的安全负荷会发生变化吗?变大还是变小?
(2)现有一根横截面为半圆(半圆的半径为R= )的柱形木材,用它截取成横截面为长方形的枕木,其长度即为枕木规定的长度l,问横截面如何截取,可使安全负荷最大?
)的柱形木材,用它截取成横截面为长方形的枕木,其长度即为枕木规定的长度l,问横截面如何截取,可使安全负荷最大?
(本小题满分12分)观察下列等式 第一个式子
第一个式子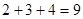 第二个式子
第二个式子 第三个式子
第三个式子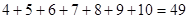 第四个式子
第四个式子
照此规律下去
(Ⅰ)写出第5个等式;
(Ⅱ)你能做出什么一般性的猜想?请用数学归纳法证明猜想.
(本小题满分12分)已知复数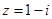 (
( 是虚数单位),函数
是虚数单位),函数 .
.
(1)若 ,求实数
,求实数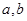 的值;
的值;
(2)解不等式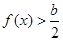 .
.