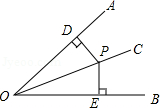
在一次机器人测试中,要求机器人从A出发到达B处.如图1,已知点A在O的正西方600cm处,B在O的正北方300cm处,且机器人在射线AO及其右侧(AO下方)区域的速度为20cm/秒,在射线AO的左侧(AO上方)区域的速度为10cm/秒.
(1) 分别求机器人沿A→O→B路线和沿A→B路线到达B处所用的时间(精确到秒);(3分)
(2) 若∠OCB=45°,求机器人沿A→C→B路线到达B处所用的时间(精确到秒);(3分)
(3) 如图2,作∠OAD=30°,再作BE⊥AD于E,交OA于P.试说明:从A出发到达B处,机器人沿A→P→B路线行进所用时间最短.(3分)
(参考数据: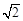 ≈1.414,
≈1.414,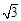 ≈1.732,
≈1.732, ≈2.236,
≈2.236, ≈2.449)
≈2.449)
某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:

(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上,
求证: .
请你补全已知和求证,并写出证明过程.
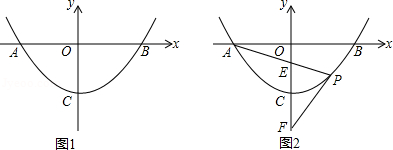
抛物线 与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若 .
①求该抛物线的解析式;
②若D是抛物线上一点,满足 ,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时, 是否为定值?若是,试求出该定值;若不是,请说明理由.
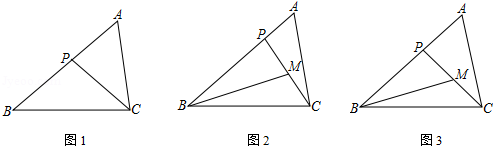
在△ABC中,P为边AB上一点.
(1)如图1,若 ,求证: ;
(2)若M为CP的中点, .
①如图2,若 , ,求BP的长;
②如图3,若 , ,直接写出BP的长.
某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:
|
产品 |
每件售价(万元) |
每件成本(万元) |
每年其他费用(万元) |
每年最大产销量(件) |
|
甲 |
6 |
a |
20 |
200 |
|
乙 |
20 |
10 |
40+0.05x2 |
80 |
其中a为常数,且 。
(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.