(本小题满分12分)
已知函数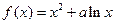 .
.
(Ⅰ)当 时,求函数
时,求函数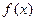 的单调递减区间;
的单调递减区间;
(Ⅱ)若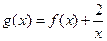 在
在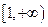 上是单调函数,求实数
上是单调函数,求实数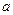 的取值范围.
的取值范围.
(本小题满分12分)
随机抽取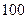 名学生,测得他们的身高(单位:
名学生,测得他们的身高(单位: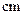 ),按照区间
),按照区间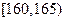 ,
,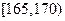 ,
, ,
,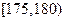 ,
, 分组,得到样本身高的频率分布直方图(如图).
分组,得到样本身高的频率分布直方图(如图).
(Ⅰ)求频率分布直方图中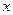 的值及身高在
的值及身高在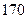
 以上的学生人数;
以上的学生人数;
(Ⅱ)将身高在 ,
,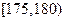 ,
, 区间内的学生依次
区间内的学生依次
记为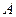 ,
,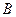 ,
,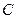 三个组,用分层抽样的方法从三个组中抽取
三个组,用分层抽样的方法从三个组中抽取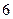 人,
人,
求从这三个组分别抽取的学生人数;
(Ⅲ)在(Ⅱ)的条件下,要从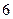 名学生中抽取
名学生中抽取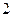 人,用列举法计算
人,用列举法计算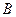 组
组
中至少有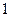 人被抽中的概率.
人被抽中的概率.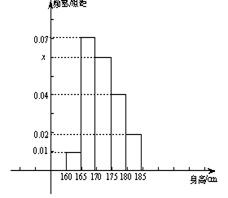
本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M、N分别为PA、BC的中点, PD⊥平面ABCD,且PD=AD=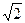 ,CD=1.
,CD=1.
(Ⅰ)证明:MN∥平面PCD;
(Ⅱ)证明:MC⊥BD.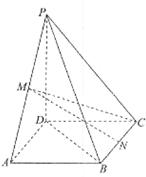
(本小题满分12分)
在假期社会实践活动中,小明参观了某博物馆,博物馆的正厅有一幅壁画.刚进入大厅时,他在点A处发现看壁画顶端点C的仰角大小为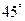 ,往正前方走4米后,在点B处发现看壁画顶端点C的仰角大小为
,往正前方走4米后,在点B处发现看壁画顶端点C的仰角大小为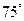 .
.
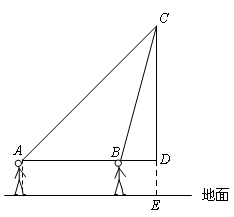
(Ⅰ) 求BC的长;
设函数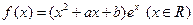 .
.
(1)若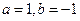 ,求函数
,求函数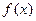 的极值;
的极值;
(2)若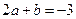 ,试确定
,试确定 的单调性;
的单调性;
(3)记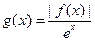 ,且
,且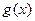 在
在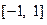 上的最大值为M,证明:
上的最大值为M,证明: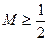 .
.