随机抽取某中学甲、乙两班各10名同学，测量他们的身高（单位：cm）获得身高数据如下：
| 甲班： |
158 |
168 |
162 |
168 |
163 |
170 |
182 |
179 |
171 |
179 |
| 乙班： |
159 |
168 |
162 |
170 |
165 |
173 |
176 |
181 |
178 |
179 |
（1）完成数据的茎叶图（以百位十位为茎，以个位为叶），并求甲班样本数据的中位数、众数；
（2）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高为176cm的同学被抽中的概率。
已知函数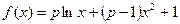
.
（1）讨论函数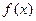
的单调性；
（2）当
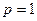时，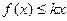
恒成立，求实数
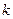的取值范围；
（3）证明：
.
已知椭圆C：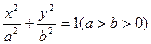
的短轴长为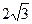
，右焦点
与抛物线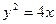
的焦点重合， 
为坐标原点
（1）求椭圆C的方程；
（2）设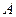
、
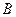是椭圆C上的不同两点，点
，且满足
，若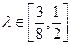
，求直线AB的斜率的取值范围.
济南市开展支教活动，有五名教师被随机的分到A、B、C三个不同的乡镇中学，且每个乡镇中学至少一名教师，
（1）求甲乙两名教师同时分到一个中学的概率；
（2）求A中学分到两名教师的概率；
（3）设随机变量X为这五名教师分到A中学的人数，求X的分布列和期望．
在数列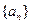
中，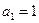
，并且对于任意n∈N*，都有
．
（1）证明数列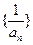
为等差数列，并求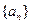的通项公式；
（2）设数列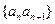
的前n项和为
，求使得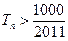
的最小正整数
.
已知矩形
与正三角形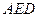
所在的平面互相垂直， 
、
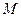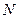分别为棱
、
的中点，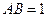
,
，
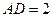(1)证明：直线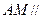
平面
；
(2)求二面角
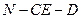的大小．