某单位拟建一个扇环面形状的花坛(如图所示)，该扇环面是由以点
为圆心的两个同心圆弧和延长后通过点的两条直线段围成．按设计要求扇环面的周长为30米，其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
，圆心角为
（弧度）．
（1）求关于的函数关系式；
（2）已知在花坛的边缘(实线部分)进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用的比为
，求关于的函数关系式，并求出为何值时，取得最大值？
（本小题满分12分）
某高中社团进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查，若开通“微博”的称为“时尚族”，否则称为“非时尚族”。通过调查分别得到如图1所示统计表如图2所示各年龄段人数频率分布直方图：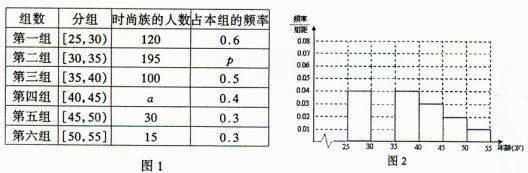
请完成下列问题：
（1）补全频率分布直方图，并求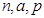
的值；
（2）从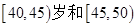
岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛，其中选取3人作为领队，求选取的3名领队年龄在
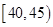岁的人数为X，求X的分布列和期望E（X）。
（本小题满分12分）
如图，在四棱锥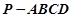
中，侧棱
底面
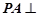，底面为矩形，
，
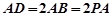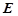为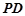
的上一点，且
，
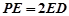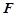为PC的中点.
（Ⅰ）求证：
平面AEC；
（Ⅱ）求二面角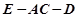
的余弦值.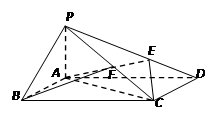
（本小题满分12分）
已知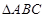
中，
、
、
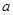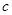是三个内角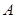
、
、
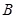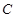的对边，关于
的不等式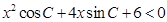
的解集是空集．
（1）求角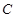的最大值；
（2）若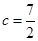
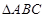，的面积
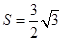，求当角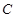取最大值时
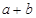的值．
（本小题满分10分）选修4－5：不等式选讲
设函数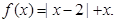
（1）求函数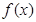
的值域；（2）若
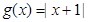，求
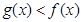成立时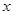
的取值范围。
（本小题满分10分）选修4－4：极坐标与参数方程
已知曲线
的极坐标方程为
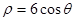，曲线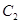
的极坐标方程为
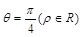，曲线
，
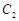相交于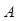
，
两点．（1）把曲线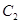，的极坐标方程转化为直角坐标方程；
（2）求弦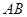
的长度．