将形如 的符号称二阶行列式,现规定
的符号称二阶行列式,现规定 , 函数
, 函数 =
= 在一个周期内的图象如图所示,
在一个周期内的图象如图所示,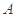 为图象的最高点,
为图象的最高点, 、
、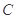 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形。
为正三角形。
(1)求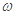 的值及函数
的值及函数 的单调递增区间;
的单调递增区间;
(2)若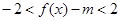 ,在
,在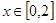 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
(理)函数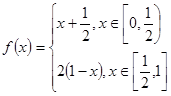 ,
,
定义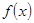 的第
的第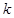 阶阶梯函数
阶阶梯函数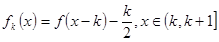 ,其中
,其中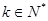 ,
,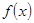 的各阶梯函数图像的最高点
的各阶梯函数图像的最高点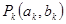 ,最低点
,最低点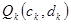
(1)直接写出不等式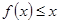 的解;
的解;
(2)求证:所有的点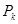 在某条直线
在某条直线 上.
上.
(3)求证:点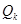 到(2)中的直线
到(2)中的直线 的距离是一个定值.
的距离是一个定值.
已知直角坐标平面内点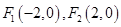 ,一曲线
,一曲线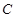 经过点
经过点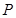 ,且
,且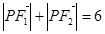
(1)求曲线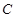 的方程;
的方程;
(2)设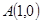 ,若
,若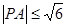 ,求点
,求点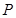 的横坐标的取值范围.
的横坐标的取值范围.
关于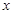 的不等式
的不等式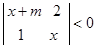 的解集为
的解集为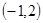 。
。
(1)求实数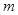 的值;
的值;
(2)若实系数一元二次方程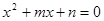 的一个根
的一个根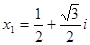 ,求
,求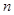 .
.
、已知锐角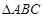 中,三个内角为
中,三个内角为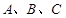 ,向量
,向量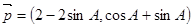 ,
,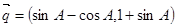 ,
,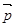 ‖
‖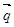 ,求
,求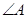 的大小.
的大小.
(本题18分,第(1)小题4分;第(2)小题6分;第(3)小题8分)
如图,已知椭圆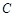 :
: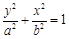
 过点
过点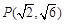 ,上、下焦点分别为
,上、下焦点分别为 、
、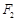 ,
,
向量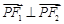 .直线
.直线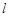 与椭圆交于
与椭圆交于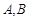 两点,线段
两点,线段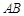 中点为
中点为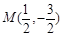 .
.
(1)求椭圆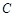 的方程;
的方程;
(2)求直线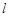 的方程;
的方程;
(3)记椭圆在直线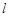 下方的部分与线段
下方的部分与线段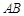 所围成的平面区域(含边界)为
所围成的平面区域(含边界)为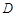 ,若曲线
,若曲线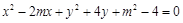 与区域
与区域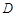 有公共点,试求
有公共点,试求 的最小值.
的最小值.