设向量
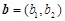 ,定义一种向量积
,定义一种向量积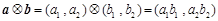 .
.
已知向量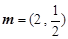 ,
,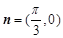 ,点
,点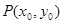 为
为 的图象上的动点,点
的图象上的动点,点 为
为 的图象上的动点,且满足
的图象上的动点,且满足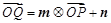 (其中
(其中 为坐标原点).
为坐标原点).
(1)请用 表示
表示 ;
;
(2)求 的表达式并求它的周期;
的表达式并求它的周期;
(3)把函数 图象上各点的横坐标缩小为原来的
图象上各点的横坐标缩小为原来的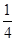 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象.设函数
的图象.设函数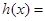
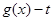
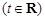 ,试讨论函数
,试讨论函数 在区间
在区间 内的零点个数.
内的零点个数.
已知函数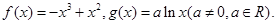 。
。
(I)求f(x)的单调区间;
(II)若对任意x∈[1,e],使得g(x)≥-x2+(a+2)x恒成立,求实数a的取值范围;
(III)设F(x)= ,曲线y=F(x)上是否总存在两点P,Q,使得△POQ是以O(O为坐标原点)为钝角柄点的钝角三角开,且最长边的中点在y轴上?请说明理由。
,曲线y=F(x)上是否总存在两点P,Q,使得△POQ是以O(O为坐标原点)为钝角柄点的钝角三角开,且最长边的中点在y轴上?请说明理由。
已知直线 ,圆O:
,圆O: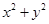 =36(O为坐标原点),椭圆C:
=36(O为坐标原点),椭圆C: =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e= ,直线l被圆O截得的弦长与椭圆的长轴长相等。
,直线l被圆O截得的弦长与椭圆的长轴长相等。
(I)求椭圆C的方程;(II)过点(3,0)作直线l,与椭圆C交于A,B两点设 (O是坐标原点),是否存在这样的直线l,使四边形为ASB的对角线长相等?若存在 ,求出直线l的方程,若不存在,说明理由。
(O是坐标原点),是否存在这样的直线l,使四边形为ASB的对角线长相等?若存在 ,求出直线l的方程,若不存在,说明理由。
如图所示,多面体FE-ABCD中,ABCD和ACFE都是直角梯形,DC∥AB,AE∥CF,平面ACFE⊥平面ABCD,AD=DC=CF=2AE=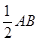 ,∠ACF=∠ADC=
,∠ACF=∠ADC=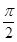 。
。
(I)求证:BC⊥平面ACFE;
(II)求二面角B-FE-D的平面角的余弦值。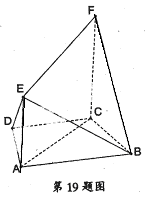
第11届全国人大五次会议于2012年3月5日至3月14日在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语。
(I)根据以上数据完成以下2X2列联表:
并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?
(II)若从会俄语的记者中随机抽取3人成立一个小组,则小组中既有男又有女的概率是多少?
(III)若从14名女记者中随机抽取2人担任翻译工作,记会俄语的人数为 ,求
,求 的期望。
的期望。
已知数列{an}的各项均为正数,其前n项和为Sn,且 -1,
-1, ,数列
,数列 ,
, ,
, ……,
……,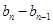 是首项为1,公比为
是首项为1,公比为 的等比数列。
的等比数列。
(I)求证:数列{an}是等差数列;
(II)若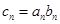 ,求数列{cn}的前n项和Tn。
,求数列{cn}的前n项和Tn。