(本小题满分13分)已知函数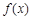 满足
满足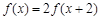 ,且当
,且当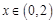 时,
时,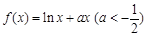 ,当
,当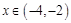 时,
时,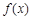 的最大值为
的最大值为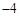 .
.
(1)求实数a的值;
(2)设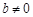 ,函数
,函数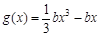 ,
,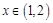 .若对任意
.若对任意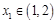 ,总存在
,总存在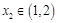 ,使
,使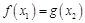 ,求实数b的取值范围.
,求实数b的取值范围.
(本小题满分13分)某高校在上学期依次举行了“法律、环保、交通”三次知识竞赛活动,要求每位同学至少参加一次活动.该高校2014级某班50名学生在上学期参加该项活动的次数统计如图所示
(1)从该班中任意选两名学生,求他们参加活动次数不相等的概率.
(2)从该班中任意选两名学生,用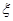 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量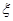 的分布列及数学期望
的分布列及数学期望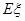 .
.
(3)从该班中任意选两名学生,用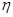 表示这两人参加活动次数之和,记“函数
表示这两人参加活动次数之和,记“函数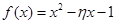 在区间(3,5)上有且只有一个零点”为事件A,求事件A发生的概率.
在区间(3,5)上有且只有一个零点”为事件A,求事件A发生的概率.
(本小题满分10分)以下是搜集到的开封市祥符区新房屋的销售价格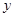 (万元)和房屋的面积
(万元)和房屋的面积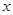 (
(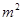 )的数据: 已知变量
)的数据: 已知变量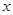 和
和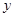 线性相关。
线性相关。
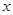 |
80 |
95 |
100 |
110 |
115 |
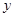 |
18.4 |
21.6 |
23.2 |
24.8 |
27 |
(Ⅰ)求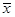 、
、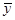 ,及线性回归方程;
,及线性回归方程;
(Ⅱ)据(Ⅰ)的结果估计当房屋面积为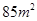 时的销售价格。
时的销售价格。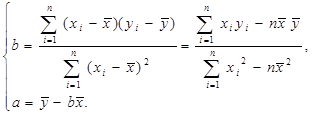
(本小题满分9分)已知 是复数,若
是复数,若 为实数(
为实数(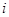 为虚数单位),且
为虚数单位),且 为纯虚数.
为纯虚数.
(1)求复数 ;
;
(2)若复数 在复平面上对应的点在第四象限,求实数
在复平面上对应的点在第四象限,求实数 的取值范围
的取值范围
(本小题满分13分)已知函数 ..
..
(Ⅰ)若 ,求函数
,求函数 的最大值;
的最大值;
(Ⅱ)令 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅲ)若 ,正实数
,正实数 满足
满足 ,证明
,证明 .
.