为了解某校学生的视力情况，现采用随机抽样的方式从该校的A，B两班中各抽5名学生进行视力检测．检测的数据如下：
A班5名学生的视力检测结果：4.3，5.1，4.6，4.1，4.9.
B班5名学生的视力检测结果：5.1，4.9，4.0，4.0，4.5.
（1）分别计算两组数据的平均数，从计算结果看，哪个班的学生视力较好？
（2）由数据判断哪个班的5名学生视力方差较大？（结论不要求证明）
（3）现从A班的上述5名学生中随机选取3名学生，用X表示其中视力大于4.6的人数，求X的分布列和数学期望.
一袋中装有5只球，编号为1，2，3，4，5，在袋中同时取3只，以
表示取出的3只球中的最大号码，写出随机变量的分布列．
盒中装有大小相等的球10个，编号分别为0，1，2，…，9，从中任取1个，观察号码是“小于5”“等于5”“大于5”三类情况之一．规定一个随机变量，并求其概率分布列．
某一中学生心理咨询中心服务电话接通率为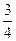
，某班3名同学商定明天分别就同一问题询问该服务中心．且每人只拨打一次，求他们中成功咨询的人数
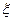的分布列．
某射手有5发子弹，射击一次命中概率为0.9，如果命中就停止射击，否则一直到子弹用尽，求耗用子弹数
的分布列．
一批产品共100件，其中有10件是次品，为了检验其质量，从中以随机的方…式选取5件，求在抽取的这5件产品中次品数分布列与期望值，并说明5件中有3件以上（包括3件）为次品的概率．（精确到0．001）