如图所示,等腰△ABC的底边 ,高CD=3,点E是线段BD上异于点B,D的动点,点F在BC边上,且EF⊥AB,现沿EF将△BEF折起到△PEF的位置,使PE⊥AC,记BE=x,V(x)表示四棱锥P﹣ACFE的体积.
,高CD=3,点E是线段BD上异于点B,D的动点,点F在BC边上,且EF⊥AB,现沿EF将△BEF折起到△PEF的位置,使PE⊥AC,记BE=x,V(x)表示四棱锥P﹣ACFE的体积.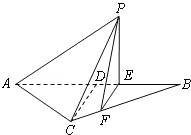
(1)求V(x)的表达式;
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值.
设函数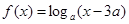
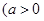 且
且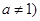 ,当点
,当点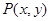 是函数
是函数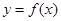 图象上的点时,点
图象上的点时,点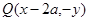 是函数
是函数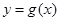 图象上的点.
图象上的点.
(1)写出函数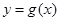 的解析式;
的解析式;
(2)若当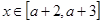 时,恒有
时,恒有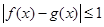 ,试确定
,试确定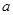 的取值范围.
的取值范围.
在直三棱柱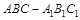 中,
中,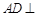 平面
平面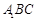 ,其垂足
,其垂足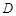 落在直线
落在直线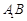 上.
上.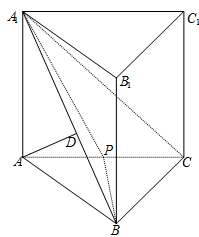
(Ⅰ)求证: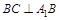 ;
;
(Ⅱ)若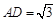 ,
,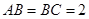 ,
,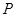 为
为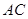 的中点,求三棱锥
的中点,求三棱锥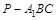 的体积.
的体积.
已知函数 .
. 当
当 时,解不等式
时,解不等式 ;
; 若存在实数
若存在实数 ,使得不等式
,使得不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知函数f(x)=ax2+x-a,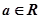 .
.
(1)若函数f(x)有最大值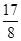 ,求实数a的值;
,求实数a的值;
(2)当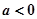 时,解不等式f(x)>1.
时,解不等式f(x)>1.
已知z,y之间的一组数据如下表:
| x |
1 |
3 |
6 |
7 |
8 |
| y |
1 |
2 |
3 |
4 |
5 |
(1)从x ,y中各取一个数,求x+y≥10的概率;
(2)对于表中数据,甲、乙两同学给出的拟合直线分别为 与
与 ,试利用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好.
,试利用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好.