如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=∠BFD．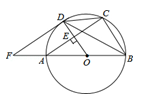
（1）求证：FD是⊙O的一条切线；
（2）若AB=10， AC=8，求DF的长．
如图，一楼房AB后有一假山，其坡度为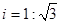
，山坡坡面上E点处有一休息亭，测的假山坡脚C与楼房水平距离BC＝25米，与亭子距离CE＝20米，小丽从楼房顶测得E点的俯角为45°，求楼房AB的高．（注：坡度i是指坡面的铅直高度与水平宽度的比）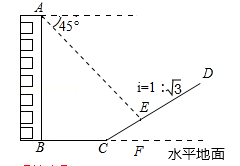
如图，在△ABC中，D，E分别是AB，AC的中点，过点E作EF∥AB，交BC于点F．
（1）求证：四边形DBFE是平行四边形；
（2）当△ABC满足什么条件时，四边形DBFE是菱形？为什么？
为了了解学生在一年中的课外阅读量，九（1）班对九年级800名学生采用随机抽样的方式进行了问卷调查，调查的结果分为四种情况：A 10本以下，B 10～15本，C 16～20本，D 20本以上．根据调查结果统计整理并制作了如图所示的两幅统计图表：
（1）在这次调查中一共抽查了名学生；
（2）表中x，y的值分别为：x=，y=；
（3）在扇形统计图中，C部分所对应的扇形的圆心角是度；
（4）根据抽样调查结果，请估计九年级学生一年阅读课外书20本以上的学生人数．
小武新家装修，在装修客厅时，购进彩色地砖和单色地砖共100块，共花费5600元．已知彩色地砖的单价是80元/块，单色地砖的单价是40元/块．
（1）两种型号的地砖各采购了多少块？
（2）如果厨房也要铺设这两种型号的地砖共60块，且采购地砖的费用不超过3200元，那么彩色地砖最多能采购多少块？
