对于三次函数
 。
。
定义:(1)设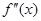 是函数
是函数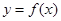 的导数
的导数 的导数,若方程
的导数,若方程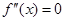 有实数解
有实数解 ,则称点
,则称点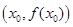 为函数
为函数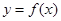 的“拐点”;
的“拐点”;
定义:(2)设 为常数,若定义在
为常数,若定义在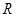 上的函数
上的函数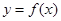 对于定义域内的一切实数
对于定义域内的一切实数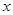 ,都有
,都有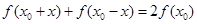 成立,则函数
成立,则函数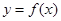 的图象关于点
的图象关于点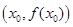 对称。
对称。
己知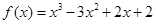 ,请回答下列问题:
,请回答下列问题:
(1)求函数 的“拐点”
的“拐点”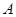 的坐标
的坐标
(2)检验函数 的图象是否关于“拐点”
的图象是否关于“拐点”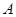 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数 ,使得它的“拐点”是
,使得它的“拐点”是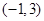 (不要过程)
(不要过程)
(本小题满分12分)
已知函数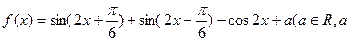 为常数).
为常数).
(1)求函数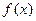 的最小正周期;(2)求函数
的最小正周期;(2)求函数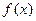 的单调递增区间;
的单调递增区间;
(3) 若 时,
时,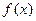 的最小值为
的最小值为 ,求
,求 的值.
的值.
(本小题满分10分)选修4-5:不等式选讲
(I)已知 都是正实数,求证:
都是正实数,求证: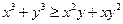 ;
;
(II)设函数 ,解不等式
,解不等式 .
.
已知A、B是圆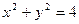 上满足条件
上满足条件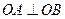 的两个点,其中O是坐标原点,
的两个点,其中O是坐标原点, 分别过A、B作
分别过A、B作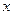 轴的垂线段,交椭圆
轴的垂线段,交椭圆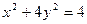 于
于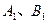 点,动点P满足
点,动点P满足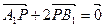 .(1)求动点P的轨迹方程;(2)设S1和S2
.(1)求动点P的轨迹方程;(2)设S1和S2 分别表示
分别表示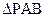 和
和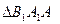 的面积,当点P在x轴的上方,点A在x轴的下方时,求
的面积,当点P在x轴的上方,点A在x轴的下方时,求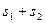 的最大值。
的最大值。
已知抛物线 上一点M(1,1),动弦ME、MF分别交
上一点M(1,1),动弦ME、MF分别交 轴与A、B两点,且MA=MB
轴与A、B两点,且MA=MB 。证明:直线EF的斜率为定值。
。证明:直线EF的斜率为定值。
已知函数 ,(1)求
,(1)求 的单调区间;(2)若
的单调区间;(2)若 ,求
,求 在区间
在区间 上的最值;
上的最值;