已知函数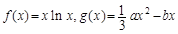
，其中a，b∈R
(1)求函数f(x)的最小值；
(2)当a＞0，且a为常数时，若函数h(x)＝x[g(x)＋1]对任意的x1＞x2≥4，总有
成立，试用a表示出b的取值范围；
(3)当
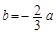时，若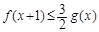
对x∈[0，＋∞)恒成立，求a的最小值.
（本小题满分12分）某厂生产的产品在出厂前都要做质量检测，每一件一等品都能通过
检测，每一件二等品通过检测的概率为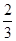
.现有10件产品，其中6件是一等品，4件是二等
品.
(Ⅰ) 随机选取1件产品，求能够通过检测的概率；
(Ⅱ) 随机选取3件产品，其中一等品的件数记为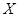
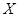，求的分布列；
(Ⅲ) 随机选取3件产品，求这三件产品都不能通过检测的概率.
（本小题满分12分）已知函数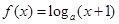
，
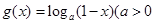，且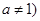
（1）求函数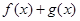
定义域
（2）判断函数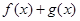的奇偶性，并说明理由.
（本小题12分）已知数列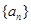
中，
，且点
在直线
上.
(1) 求数列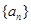的通项公式；
(2) 若函数
，求证
（本小题10分）已知圆
经过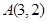
、
两点，且圆心在直线
上．
(1) 求圆的方程；
(2) 若直线
经过点
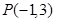且与圆相切，求直线的方程．
（本小题10分）如图已知在三棱柱ABC——A1B1C1中，AA1⊥面ABC，AC=BC，M、N、P、Q分别是AA1、BB1、AB、B1C1的中点.
(1) 求证：面PCC1⊥面MNQ；
(2) 求证：PC1∥面MNQ。