已知实数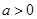 ,函数
,函数 .
.
(1)当 时,求
时,求 的最小值;
的最小值;
(2)当 时,判断
时,判断 的单调性,并说明理由;
的单调性,并说明理由;
(3)求实数 的范围,使得对于区间
的范围,使得对于区间 上的任意三个实数
上的任意三个实数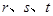 ,都存在以
,都存在以 为边长的三角形.
为边长的三角形.
在 中,三边
中,三边 、
、 、
、 对角分别为
对角分别为 、
、 、
、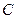 ,且
,且
(1)求角 的余弦值;(2)若
的余弦值;(2)若 ,且
,且 ,求
,求 和
和 的值.
的值.
已知函数 ,
, .(1)求函数
.(1)求函数 在
在 内的单调递增区间;
内的单调递增区间;
(2)若函数 在
在 处取到最大值,求
处取到最大值,求 的值;
的值;
(3)若 (
( ),求证:方程
),求证:方程 在
在 内没有实数解.(参考数据:
内没有实数解.(参考数据: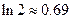 ,
,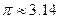 )
)
已知角 为
为 的三个内角,其对边分别为
的三个内角,其对边分别为 ,若
,若 ,
, ,
, ,且
,且 .(1)若
.(1)若 的面积
的面积 ,求
,求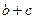 的值.(2)求
的值.(2)求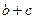 的取值范围.
的取值范围.
设函数f(x)=cos(2x+ )+sin
)+sin x.(1)求函数f(x)的最大值和最小正周期. w.w.(2)设A,B,C为
x.(1)求函数f(x)的最大值和最小正周期. w.w.(2)设A,B,C为 ABC的三个内角,若cosB=
ABC的三个内角,若cosB= ,
, ,且C为锐角,求sinA.
,且C为锐角,求sinA.
已知向量 ,向量,
,向量, 与向量
与向量 的夹角为
的夹角为 ,且
,且 ="-1" (1)求向量
="-1" (1)求向量 ; (2)设向量
; (2)设向量 =(1,0),向量
=(1,0),向量 ,其中0<
,其中0< <
<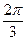 ,若
,若 =0,试求|
=0,试求| ︱的取值范围。
︱的取值范围。