(本小题满分12分)
甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率
,乙每次击中目标的概率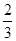 .
.
(1)记甲击中目标的次数为ξ,求ξ的概率分布列及数学期望Eξ;
(2)求甲恰好比乙多击中目标2次的概率.
已知△ABC的内角A、B、C的对边分别为a、b、c,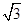 sin Ccos C-cos2C=
sin Ccos C-cos2C=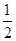 ,且c=3.
,且c=3.
(1)求角C;
(2)若向量m=(1,sin A)与n=(2,sin B)共线,求a、b的值.
设函数f(x)=ax2+(b-2)x+3(a≠0),若不等式f(x)>0的解集为(-1,3).
(1)求a,b的值;
(2)若函数f(x)在x∈[m,1]上的最小值为1,求实数m的值.
设函数f(x)=ex-ax-2.
(1)求f(x)的单调区间;
(2)若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0,求k的最大值.
某造纸厂拟建一座底面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/平方米,水池所有墙的厚度忽略不计.
(1)试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2)若由于地形限制,该池的长和宽都不能超过16米,试设计污水处理池的长和宽,使总造价最低,并求出最低总造价.
已知函数f(x)=xk+b(其中k,b∈R且k,b为常数)的图象经过A(4,2)、B(16,4)两点.
(1)求f(x)的解析式;
(2)如果函数g(x)与f(x)的图象关于直线y=x对称,解关于x的不等式:g(x)+g(x-2)>2a(x-2)+4.