如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.
小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60米,下坡路每分钟走80米,上坡路每分钟走40米,从家里到学校需10分钟,从学校到家里需15分钟.请问小华家离学校多远?
如图是图形的操作过程(四个矩形水平方向的边长均为a,竖立方向的边长均为b):将线段A1A2向右平移1个单位得到B1B2,得到封闭图形A1A2B2B1[即阴影部分如图(1)];将折线A1A2A3向右平移1个单位得到B1B2B3,得到封闭图形A1A2A3B3B2B1[即阴影部分如图(2)].
(1)在图(3)中,请你类似地画出一条有两个折点的直线,同样向右平移1个单位,从而得到1个封闭图形,并画出阴影.
(2)请你分别写出上述三个阴影部分外的面积S1=,S2=,S3=.
(3)联想与探索:如图(4),在一矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位).请你猜想空白部分草地面积是多少?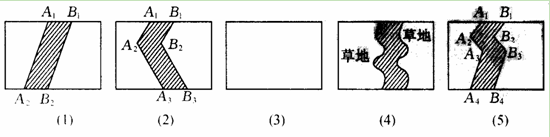
用144分米长的铁丝围成一个长方体框架,一只蚂蚁从顶点A出发,沿棱爬行,经顶点BC到达D,已知蚂蚁每分钟爬行6分米经BC比AB多用1分钟,经CD比BC少用2分钟,这个长方体框架的长宽高各是多少?
在直角三角形中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm.
(1)△ABC的面积;
(2)求CD的长?
(3)若△ABC的边AC上的中线是BE,求△ABE的面积.
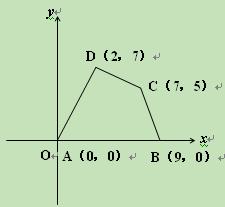
如图所示的直角坐标系中,四边形的四个顶点坐标分别是A(0,0)、B(9,0)、C(7,5)、D(2,7),求这个四边形的面积.