某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 (个) (个) |
2 |
3 |
4 |
5 |
加工的时间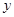 (小时) (小时) |
2.5 |
3 |
4 |
4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出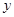 关于
关于 的线性回归方程
的线性回归方程 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工 个零件需要多少时间?
个零件需要多少时间?
参考公式:回归直线 ,其中
,其中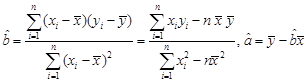 .
.
已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.
(1)求抛物线方程;
(2)过M作MN⊥FA,垂足为N,求点N的坐标
已知M(0,-2),点A在x轴上,点B在y轴的正半轴,点P在直线AB上,且满足=,·=0.
(1)当点A在x轴上移动时,求动点P的轨迹C的方程;
(2)过(-2,0)的直线l与轨迹C交于E、F两点,又过E、F作轨迹C的切线l1、l2,当l1⊥l2,求直线l的方程.
如右图所示,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B.
(1)求证:A、M、B三点的横坐标成等差数列;
(2)已知当M点的坐标为(2,-2p)时,=4,求此时抛物线的方程;
如右图所示,已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥平面AC,且PA=AD=AB=1,BC=2.
(1)求PC的长;
(2)求异面直线PC与BD所成角的余弦值的大小
如右图所示,在三棱锥A-BCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.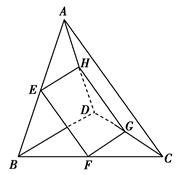
(1)求证:四边形EFGH是平行四边形;
(2)若AC=BD,求证:四边形EFGH是菱形;
(3)当AC与BD满足什么条件时,四边形EFGH是正方形