设函数 ,且
,且 ,
,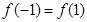 .
.
(1)求 的解析式;
的解析式;
(2)画出 的图象.
的图象.
已知函数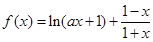 (
(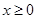 ,
,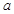 为正实数).
为正实数).
(Ⅰ)若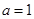 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若函数 的最小值为
的最小值为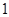 ,求
,求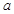 的取值范围.
的取值范围.
|
如图,在四棱锥 中,平面
中,平面 平面
平面 .底面
.底面 为矩形,
为矩形,  ,
, .
.
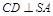 ;
;
 的大小.
的大小.

如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为 (假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(Ⅰ)求某个家庭得分为 的概率?
的概率?
(Ⅱ)若游戏规定:一个家庭的得分为参与游戏的两人得分之和,且得分大于等于8的家庭可以获得一份奖品.请问某个家庭获奖的概率为多少?
(Ⅲ)若共有5个家庭参加家庭抽奖活动.在(Ⅱ)的条件下,记获奖的家庭数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
在锐角 中,
中, ,
,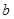 ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若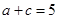 ,且
,且 ,
, ,求
,求 的值.
的值.
已知集合 ,若集合
,若集合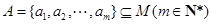 ,且对任意的
,且对任意的 ,存在
,存在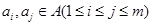 ,使得
,使得 (其中
(其中 ),则称集合
),则称集合 为集合
为集合 的一个
的一个 元基底.
元基底.
(Ⅰ)分别判断下列集合 是否为集合
是否为集合 的一个二元基底,并说明理由;
的一个二元基底,并说明理由;
① ,
, ;
;
② ,
,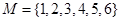 .
.
(Ⅱ)若集合 是集合
是集合 的一个
的一个 元基底,证明:
元基底,证明: ;
;
(Ⅲ)若集合 为集合
为集合 的一个
的一个 元基底,求出
元基底,求出 的最小可能值,并写出当
的最小可能值,并写出当 取最小值时
取最小值时 的一个基底
的一个基底 .
.