对某校小学生进行心理障碍测试得到如下的列联表:
| |
有心理障碍 |
没有心理障碍 |
总计 |
| 女生 |
10 |
|
30 |
| 男生 |
|
70 |
80 |
| 总计 |
20 |
|
110 |
将表格填写完整,试说明心理障碍与性别是否有关?
附:
| P(K2≥k) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| K |
2.072 |
2.076 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
设椭圆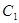 :
: 的左、右焦点分别是
的左、右焦点分别是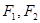 ,下顶点为
,下顶点为 ,线段
,线段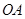 的中点为
的中点为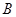 (
(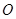 为坐标原点),如图.若抛物线
为坐标原点),如图.若抛物线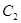 :
: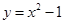 与
与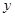 轴的交点为
轴的交点为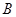 ,且经过
,且经过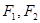 点.
点.
(Ⅰ)求椭圆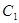 的方程;
的方程;
(Ⅱ)设 ,
,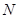 为抛物线
为抛物线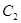 上的一动点,过点
上的一动点,过点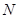 作抛物线
作抛物线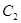 的切线交椭圆
的切线交椭圆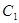 于
于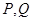 两点,求
两点,求 面积的最大值.
面积的最大值.
直四棱柱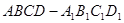 中,底面
中,底面 是等腰梯形,
是等腰梯形,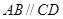 ,
,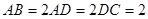 ,
,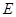 为
为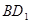 的中点,
的中点,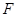 为
为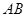 中点.
中点.
(1) 求证: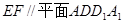 ;
;
(2) 若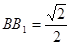 ,求
,求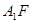 与平面
与平面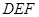 所成角的大小
所成角的大小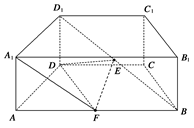
某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是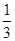 ,每次测试通过与否相互独立.规定:若前4次都没有通过测试,则第5次不能参加测试.
,每次测试通过与否相互独立.规定:若前4次都没有通过测试,则第5次不能参加测试.
(1)求该学生考上大学的概率;
(2)如果考上大学或参加完5次考试就结束,求该生至少参加四次考试的概率
已知数列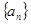 的前
的前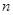 项和,
项和,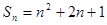 。
。
(I)求数列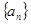 的通项公式
的通项公式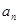 ;
;
(II)记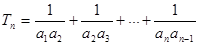 ,求
,求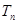
已知函数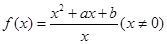 是奇函数,且满足
是奇函数,且满足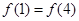
(Ⅰ)求实数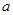 、
、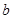 的值;
的值;
(Ⅱ)试证明函数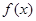 在区间
在区间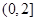 单调递减,在区间
单调递减,在区间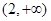 单调递增;
单调递增;
(Ⅲ)是否存在实数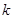 同时满足以下两个条件:1不等式
同时满足以下两个条件:1不等式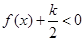 对
对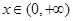 恒成立; 2方程
恒成立; 2方程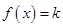 在
在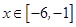 上有解.若存在,试求出实数
上有解.若存在,试求出实数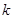 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.