已知,在△ABC中,AB=AC.过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直线a交BC边于点P(点P不与点B、点C重合),△BMN的边MN始终在直线a上(点M在点N的上方),且BM=BN,连接CN.
(1)当∠BAC=∠MBN=90°时,
①如图a,当θ=45°时,∠ANC的度数为 ;
②如图b,当θ≠45°时,①中的结论是否发生变化?说明理由;
(2)如图c,当∠BAC=∠MBN≠90°时,请直接写出∠ANC与∠BAC之间的数量关系,不必证明.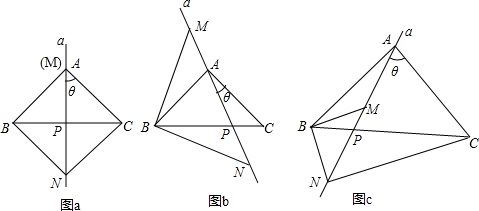
小圆盖大圆
桌子上有一个半径为1的大纸圆,另有许多直径为1的小纸圆.现在要用这些小的圆去盖住大圆,问:至少要用几个小圆?
某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价也相同.随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元.
(1)求该同学看中的随身听和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:
| 捐款(元) |
1 |
 2 2 |
3 |
4 |
| 人数 |
6 |
7 |
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.
若设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组()
A.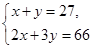 B.
B.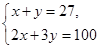 C.
C.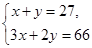 D.
D.
(2)(2005年,乌鲁木齐)为满足市民对优质教育的需求,某中学决定改变办学条件,计划拆除一部分旧校舍、建造新校舍.拆除旧校舍每平方米需80元,建造新校舍每平方米需700元.计划在年内拆除旧校舍与建造新校舍共7200平方米,在实施中为扩大绿地面积,新建校舍只完成了计划的80%,而拆除旧校舍则超过了计划的10%,结果恰好完成了原计划的拆、建总面积.
①求原计划拆、建面积各是多少平方米?
②若绿化1平方米需200元,那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米?
(1)某水果批发市场香蕉的价格如下表:
| 购买香蕉数 |
不超过 20千克 |
超过20千克但 不超过40千克 |
40千克 以上 |
| 每千克价格 |
6元 |
5元 |
4元 |
张强两次共购买香蕉50千克(第二次多于第一次),共付出264元,请问张强两次各购买香蕉多少千克.
(2)宏泰毛纺厂购进由甲、乙两种原料配成的两种材料,已知一种材料按甲:乙=5:4配料,每吨50元;另一种材料按甲:乙=3:2配料,每吨48.6元.求甲、乙两种原料的价格各是多少?
革命老区百色某芒果种植基地,去年结余500万元,估计今年可结余960万元,并且今年的收入比去年高15%,支出比去年低10%,求去年的收入与支出各是多少万元?