设函数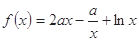
(1) 当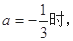 若在
若在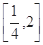 存在
存在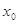 ,使得不等式
,使得不等式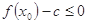 成立,求
成立,求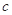 的最小值.
的最小值.
(2) 若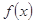 在
在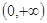 上是单调函数,求
上是单调函数,求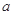 的取值范围.
的取值范围.
(参考数据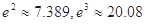 )
)
.(本小题满分12分)
已知函数f(x)=ax2+a2x+2b-a3,当x∈(-2,6)时,f(x)>0,
当x∈(-∞,-2)∪(6 ,+∞)时,f(x)<0,
,+∞)时,f(x)<0,
(1)求f(x)的解析式.
(2)求f(x)在区间[1,10]上的最值。
在数列 中,
中, ,
, (
( )
)
(1)求 ,
,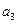 的值;
的值;
(2)求证:数列 是等比数列,并求出
是等比数列,并求出 的通项公式;
的通项公式;
(3)设 ,
, ,求
,求
在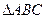 中,三角形的边长分别为1,2,a
中,三角形的边长分别为1,2,a
(1)求a的取值范围。
(2)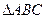 为钝角三角形,求a的范围。
为钝角三角形,求a的范围。
在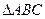 中,角
中,角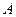 、
、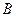 、
、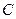 所对的边分别是
所对的边分别是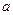 、
、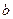 、
、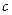 ,向量
,向量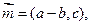
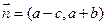 ,且
,且 与
与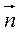 共线.
共线.
(1)求角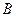 的大小;
的大小;
(2)若
在等差数列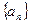 中,前三项分别为
中,前三项分别为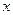 ,
,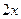 ,
,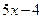 ,前
,前 项和为
项和为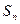 ,且
,且
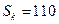 .
.
(1)求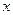 和
和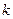 的值;
的值;
(2)设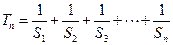 ,求满足
,求满足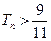 的最小正整数
的最小正整数 .
.