已知三次函数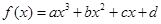 的图像关于点
的图像关于点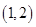 对称,
对称,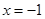 是
是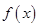 的一个极值点,且
的一个极值点,且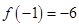 ,求函数
,求函数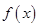 在区间
在区间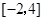 上的最值.
上的最值.
请你设计一顶帐篷,它下部的形状是高为1m的正棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示),试问当帐篷的顶点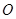 到底面中心
到底面中心 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?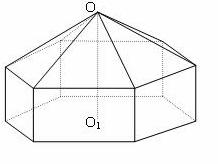
.已知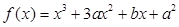 在
在 时有极值0.
时有极值0.
①求常数 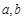 的值;
的值;
②求 的单调区间;
的单调区间;
③方程 在区间[-4,0]上有三个不同的实根时实数
在区间[-4,0]上有三个不同的实根时实数 的范围.
的范围.
(本小题满分16分)对于函数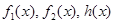 ,如果存在实数
,如果存在实数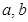 使得
使得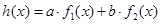 ,那么称
,那么称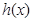 为
为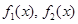 的生成函数.
的生成函数.
(Ⅰ)下面给出两组函数,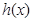 是否分别为
是否分别为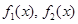 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组: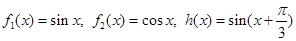 ;
;
第二组: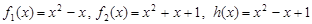 ;
;
(Ⅱ)设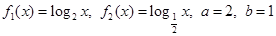 ,生成函数
,生成函数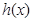 .若不等式
.若不等式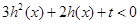 在
在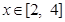 上有解,求实数
上有解,求实数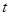 的取值范围;
的取值范围;
(Ⅲ)设 ,取
,取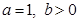 ,生成函数
,生成函数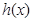 使
使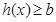 恒成立,求
恒成立,求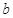 的取值范围.
的取值范围.
(本小题满分16分) 已知函数
 ,在
,在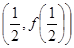 处的
处的
切线方程为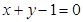 .
.
(1)求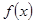 的解析式;
的解析式;
(2)设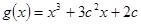
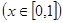 ,若对任意
,若对任意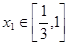 ,总存在
,总存在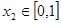 ,使得
,使得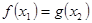 成立,求实数
成立,求实数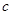 的取值范围.
的取值范围.