抛物线y2=2px(p>0)上纵坐标为-p的点M到焦点的距离为2.
(1)求p的值;
(2)如图,A,B,C为抛物线上三点,且线段MA,MB,MC 与x轴交点的横坐标依次组成公差为1的等差数列,若△AMB的面积是△BMC面积的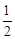 ,求直线MB的方程.
,求直线MB的方程.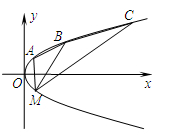
两种大小不同的钢板可按下表截成A,B,C三种规格成品: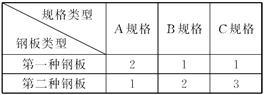
某建筑工地需A,B,C三种规格的成品分别为15,18,27块,问怎样截这两种钢板,可
得所需三种规格成品,且所用钢板张数最小.
已知点M(x1,f(x1))是函数f(x)= ,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.
,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.
(1)求切线l的方程;
(2)设l与x轴,y轴的交点分别为A、B,求△AOB周长的最小值.
设f(x)是定义域为(-∞,0)∪(0,+∞)上的奇函数且在(-∞,0)上为增函数.
(1)若m·n<0,m+n≤0,求证:f(m)+f(n)≤0;
(2)若f(1)=0,解关于x的不等式f(x2-2x-2)>0.
函数f(x)对一切实数x,y均有f(x+y)-f(y)=(x+2y+1)x成立,且f(1)=0.
(1)求f(0);
(2)求f(x);
(3)不等式f(x)>ax-5当0<x<2时恒成立,求a的取值范围.
甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x),g(x)以及任意的x≥0,当甲公司投入x万元做宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元做宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司这一新产品的开发有失败的风险,否则没有失败的风险.
(1)试解释f(0)=10,g(0)=20的实际意义;
(2)设f(x)=  x+10,g(x)=
x+10,g(x)= +20,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
+20,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?