在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):
方案一:提供8000元赞助后,每张票的票价为50元;
方案二:票价按图中的折线OAB所表示的函数关系确定.
(1)若购买120张票时,按方案一和方案二分别应付的购票款是多少?
(2)求方案二中y与x的函数关系式;
(3)至少买多少张票时选择方案一比较合算?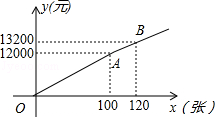
已知抛物线 (
( )与
)与 轴相交于点
轴相交于点 ,顶点为
,顶点为 .直线
.直线 分别与
分别与 轴,
轴, 轴相交于
轴相交于 两点,并且与直线
两点,并且与直线 相交于点
相交于点 .
.
(1)如图,将 沿
沿 轴翻折,若点
轴翻折,若点 的对应点
的对应点 ′恰好落在抛物线上,
′恰好落在抛物线上, ′与
′与 轴交于点
轴交于点 ,连结
,连结 ,求
,求 的值和四边形
的值和四边形 的面积;
的面积;
(2)在抛物线 (
( )上是否存在一点
)上是否存在一点 ,使得以
,使得以 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
小华早晨6点多钟去学校,去时看了一下手表,发现时针与分针的夹角为 度(0<
度(0< <180,
<180, 为整数),到了学校,他又看了一下手表,发现此时还不到7点钟,且时针与分针的夹角为也为
为整数),到了学校,他又看了一下手表,发现此时还不到7点钟,且时针与分针的夹角为也为 度,若小华去学校途中所用的时间是10的整数倍,那么,小华去学校途中所用的时间是多少?
度,若小华去学校途中所用的时间是10的整数倍,那么,小华去学校途中所用的时间是多少?
设x1、x2是方程x2-6x+a=0的两个根,以x1、x2为腰和底边的等腰三角形只可以画出一个.试求a的取值范围.
已知⊙ 的半径为1,以
的半径为1,以 为原点,建立如图所示的直角坐标系.有一个正方形
为原点,建立如图所示的直角坐标系.有一个正方形 ,顶点
,顶点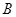 的坐标为(
的坐标为( ,0),顶点
,0),顶点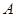 在
在 轴上方,顶点
轴上方,顶点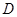 在⊙
在⊙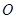 上运动.
上运动.
(1)当点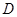 运动到与点
运动到与点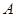 、
、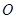 在一条直线上时,
在一条直线上时,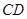 与⊙
与⊙ 相切吗?如果相切,请说明理由,并求出
相切吗?如果相切,请说明理由,并求出 所在直线对应的函数表达式;如果不相切,也请说明理由;
所在直线对应的函数表达式;如果不相切,也请说明理由;
(2)设点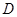 的横坐标为
的横坐标为 ,正方形
,正方形 的面积为
的面积为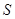 ,求出
,求出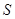 与
与 的函数关系式,并求出
的函数关系式,并求出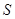 的最大值和最小值.
的最大值和最小值.
已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.