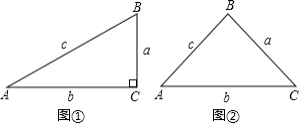
如图①, 在 中, 以下是小亮探究 与 之间关系的方法:
,
,
根据你掌握的三角函数知识 . 在图②的锐角 中, 探究 、 、 之间的关系, 并写出探究过程 .
探索规律:观察下面由※组成的图案和算式,并解答问题
(
 )试猜想
)试猜想 ;
;(
 )试猜想
)试猜想 =;
=; (
 )请用上述规律计算:
)请用上述规律计算: (请算出最后数值哦!)
(请算出最后数值哦!)
某区教育局为了了解学生参加阳光体育活动的情况,对某校学生进行随机抽样 调查,其中一个问题是“你平均每天参加阳光体育活动的时间是多少?”,共有4个选项:
调查,其中一个问题是“你平均每天参加阳光体育活动的时间是多少?”,共有4个选项:
A. 小时以上 B.
小时以上 B. ~
~ 小时 C.
小时 C. ~
~ 小时 D.
小时 D. 小时以下
小时以下
图1、2是根据调查结果绘制的两幅不完整的统计图,

请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图
 中将选项B的部分补充完整;
中将选项B的部分补充完整; (3)若该校有
 名学生,你估计全校可能有多少名学
名学生,你估计全校可能有多少名学
生平均每天参加体育活动的时间在 小时以下.
小时以下.
下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.
解:根据题意可画出图,
∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.
解下列方程:(1)

(2)
 .
.
先化简,再求值: 的值,其中
的值,其中 ,
, .
.