为了解“数学思想作文对学习数学帮助有多大？”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查，并将调查得到的数据用下面的扇形图和表来表示（图、表都没制作完成）．
| 选项 |
帮助很大 |
帮助较大 |
帮助不大 |
几乎没有帮助 |
| 人数 |
a |
543 |
269 |
b |
根据图、表提供的信息．
（1）请问：这次共有多少名学生参与了问卷调查？
（2）算出表中a、b的值．
（注：计算中涉及到的“人数”均精确到1）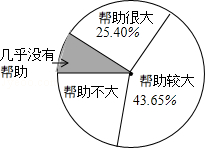
解不等式组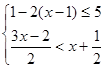
，并把解集在数轴上表示出来．
计算：
．
已知：正方形ABCD的边长为2，⊙O交正方形ABCD的对角线AC所在直线于点T，连结TO交⊙O于点S，连结AS．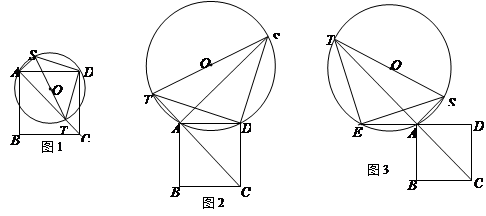
如图1，当⊙O经过A、D两点且圆心O在正方形ABCD内部时，连结DT、DS．
①试判断线段DT、DS的数量关系和位置关系；②求AS＋AT的值；如图2，当⊙O经过A、D两点且圆心O在正方形ABCD外部时，连结DT、DS．求AS－AT的值；
如图3，延长DA到点E，使AE=AD，当⊙O经过A、E两点时，连结ET、ES．
根据（1）、（2）计算，通过观察、分析，对线段AS、AT的数量关系提出问题并解答．
如图，已知一次函数
的图象与
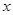轴交于点A，与二次函数
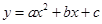的图象交于
轴上的一点B，二次函数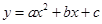的图象与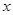轴只有唯一的交点C，且OC=2．
求二次函数
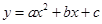的解析式；设一次函数
的图象与二次函数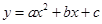的图象的另一交点为D，已知P为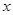轴上的一个动点，且△PBD为直角三角形，求：点P的坐标．
如图，在直角坐标系中放入一个矩形纸片OABC，将矩形纸片OABC翻折后，使点B恰好落在x轴上，记为D，折痕为CE，且OA=15，sin∠EDA=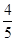
．
求D点的坐标；
求折痕CE所在直线的解析式．