在等差数列{an}和等比数列{bn}中,a1=b1=1,b4=8,{an}的前10项和S10=55.
(1)求an和bn;
(2)现分别从{an}和{bn}的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值
相等的概率.
给出下列四个结论:
(1)如图 中,
中,
 是斜边
是斜边 上的点,
上的点,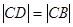 .以
.以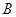 为起点任作一条射线
为起点任作一条射线 交
交 于
于 点,则
点,则 点落在线段
点落在线段 上的概率是
上的概率是 ;
;
(2)设某大学的女生体重 与身高
与身高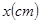 具有线性相关关系,根据一组样本数据
具有线性相关关系,根据一组样本数据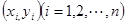 ,用最小二乘法建立的线性回归方程为
,用最小二乘法建立的线性回归方程为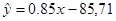 ,则若该大学某女生身高增加
,则若该大学某女生身高增加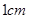 ,则其体重约增加
,则其体重约增加 ;
;
(3)若 是定义在
是定义在 上的奇函数,且满足
上的奇函数,且满足 ,则函数
,则函数 的图像关于
的图像关于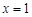 对称;
对称;
(4)已知随机变量 服从正态分布
服从正态分布 则
则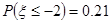 .
.
其中正确结论的序号为
(本小题满分10分)选修4-5:不等式选讲
已知函数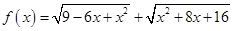
(1)解不等式 ;
;
(2)设函数 ,若不等式
,若不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分10分)选修4—4;坐标系与参数方程.
已知曲线 :
: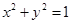 ,将曲线
,将曲线 上的点按坐标变换
上的点按坐标变换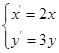 得到曲线
得到曲线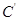 ;以直角坐标系原点为极点,
;以直角坐标系原点为极点,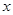 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线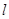 的极坐标系方程是
的极坐标系方程是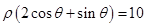 .
.
(1)写出曲线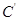 和直线
和直线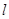 的普通方程;
的普通方程;
(2)求曲线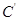 上的点
上的点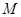 到直线
到直线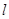 距离的最大值及此时点
距离的最大值及此时点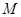 的坐标.
的坐标.
选修4—1:几何证明选讲
如图,在正 中,点
中,点 分别在边
分别在边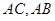 上,且
上,且 ,
,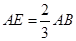 ,
,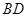 与
与 交于点
交于点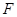 .
.
(1)求证: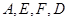 四点共圆;
四点共圆;
(2)若正 的边长为2,求点
的边长为2,求点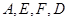 所在圆的半径.
所在圆的半径.
(本小题满分12分)己知函数
 .
.
(1)讨论函数 的单调区间;
的单调区间;
(2)设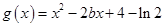 ,当
,当 时,若对任意的
时,若对任意的 都有
都有 ,求实数
,求实数 的取值范围;
的取值范围;
(3)求证: .
.