给出下列四个结论：
（1）如图
中，
是斜边
上的点，
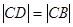．以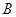
为起点任作一条射线
交于
点，则点落在线段
上的概率是
；
（2）设某大学的女生体重
与身高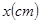
具有线性相关关系，根据一组样本数据
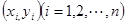，用最小二乘法建立的线性回归方程为
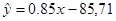，则若该大学某女生身高增加
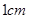，则其体重约增加
；
（3）若
是定义在
上的奇函数，且满足
，则函数的图像关于
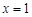对称;
（4）已知随机变量
服从正态分布
则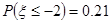
．
其中正确结论的序号为
（本小题满分14分）
已知数列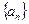
中，a1=3，a2=5，其前n项和Sn满足
令
(Ⅰ)求数列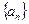的通项公式：
(Ⅱ)若
，求证：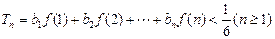
．（本小题满分14分）
如图所示，在直角梯形ABCD中，
，曲线段.DE上
任一点到A、B两点的距离之和都相等．
(Ⅰ) 建立适当的直角坐标系，求曲线段DE的方程；
(Ⅱ) 过C能否作-条直线与曲线段DE 相交，且所
得弦以C为中点，如果能，求该弦所在的直线
的方程；若不能，说明理由．
（本小题满分14分）
为了进一步实现节能，在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外
墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热
层建造成本为6万元。该建筑物每年的能源消耗费用C（单位：万元）。与隔热层
厚度x（单位：cm）满足关系：
，若不建隔热层，每年能源消耗费用为8万元；设f(x)为
隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时，总费用f(x）达到最小，并求最小值。
（本小题满分14分）
如图，在四棱锥P-ABCD中，PD上⊥平面ABCD，AD⊥CD，且BD平分∠ADC，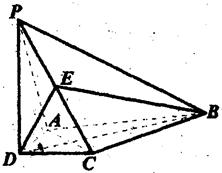
E为PC的中点，AD=CD=l，BC=PC，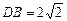
(Ⅰ)证明PA∥平面BDE；
(Ⅱ)证明AC⊥平面PBD：
(Ⅲ)求四棱锥P-ABCD的体积，
（本小题满分12分）
在平面直角坐标系xOy中，点A(-l，-2）、B(2，3)、C(-2，-1)。
(Ⅰ)求以线段AB、AC为邻边的平行四边形两条对角线的长：
(Ⅱ)设实数t满足
，求t的值。