如图所示,质量m=50kg的运动员(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=5.0m处的D点有一只救生圈,O、A、C、D各点均在同一竖直面内。若运动员抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定初速度跃出,当摆到O点正下方的B点时松开手,最终恰能落在救生圈内。(sin37°=0.6,cos37°=0.8,g=10m/s2)求: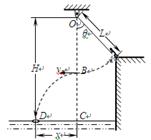
(1)运动员经过B点时速度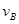 的大小;
的大小;
(2)运动员经过B点时绳子的拉力大小;
(3)运动员从A点跃出时的动能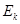 。
。
在“用单摆测定重力加速度”的实验中①测摆长时,若正确测出悬线长l和摆球直径d,则摆长为;②测周期时,当摆球经过位置时开始计时并计数1次,测出经过该位置N次(约60~100次)的时间为t,则周期为。
此外,请你从下列器材中选用所需器材,再设计一个实验,粗略测出重力加速度g,并参照示例填写下表(示例的方法不能再用)
A.天平;B.刻度尺;C.弹簧秤;D.电磁打点计时器;E.带夹子的重锤;
F.纸带;G.导线若干;H.铁架台;I.低压交流电源;J.低压直流电源;
G.小车;K.螺旋测微器;M.斜面(高度可调,粗糙程度均匀)
| 所选器材 (只填器材序号) |
简述实验方法 (不要求写出具体步骤) |
|
| 示例 |
B、D、E、F、G、H、I |
安装仪器,接通电源,让纸带随重锤竖直下落。 用刻度尺测出所需数据,处理数据,得出结果 |
| 实验 设计 |
(
在"用单摆测重力加速度"的实验中,
(1)某同学的操作步骤为:
a.取一根细线,下端系住直径为
的金属小球,上端固定在铁架台上
b.用米尺量得细线长度
c.在摆线偏离竖直方向5°位置释放小球
d.用秒表记录小球完成
次全振动的总时间t,得到周期
e.用公式
计算重力加速度
按上述方法得出的重力加速度值与实际值相比(选填"偏大"、"相同"或"偏小")。
(2)已知单摆在任意摆角
时的周期公式可近似为
,式中
为摆角趋近于0°时的周期,
为常数。为了用图像法验证该关系式,需要测量的物理量有;若某同学在实验中得到了如图所示的图线,则图像中的横轴表示。

为了测定光在透明的有机玻璃中的传播速度,实验室中可提供的器材有:矩形有机玻璃砖(长约40 cm)、秒表、平行光光源、刻度尺、三角板、白纸、大头针若干等.已知真空中的光速是c=3.00×108 m/s.
(1)请从上述器材中选出必需的器材来测量光速;
(2)说明测量光速的方法和要测量的量,并给出计算光速的公式.
某同学在测定一厚度均匀的圆形玻璃的折射率时,先在白纸上作一与圆形玻璃同半径的圆,圆心为O,将圆形玻璃平放在白纸上,使其边界与所画的圆重合.在玻璃一侧竖直插两枚大头针P1和P2.在另一侧再先后插两枚大头针P3和P4,使从另一侧隔着玻璃观察时,大头针P4、P3和P2、P1的像恰在一直线上.移去圆形玻璃和大头针后,在图13-1-24中画出:
图13-1-24
(1)沿P1、P2连线方向的入射光线通过圆形玻璃后的传播方向;
(2)光线在玻璃内的传播方向;
(3)过光线的入射点作法线,标出入射角θ1和折射角θ2;
(4)写出计算玻璃折射率的公式.
由于实验室中矩形玻璃砖的数量不够,部分同学需改用半圆形玻璃砖做“测定玻璃的折射率”实验.实验步骤如下,请把步骤填写完整并回答注意问题.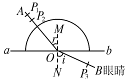
图13-1-25
(1)
| A.如图13-1-25,在一张白纸上画一直线ab作为玻璃砖的一个界面,标出点O |
| B.过O点画一线段OA,在OA上垂直地插两枚大头针P1、P2 |
| C.放上玻璃砖,使O点正好处于圆心的位置 |
| D.透过玻璃砖观察大头针P1、P2的像,调整视线方向,直到________的像完全被________挡住 |
E.在观察的这一侧插一大头针P3,使_________挡住_________的像
F.标出P3的位置
G.移去玻璃砖和大头针,连接OP3,作过O点与ab垂直的直线MN
H.用量角器量出∠MOA和∠NOB两角的大小.根据光路可逆性,当光线从空气射向玻璃砖时,∠NOB为入射角,记为i,∠MOA为折射角,记为r
Ⅰ.代入折射定律,得到玻璃的折射率n=____________
(2)为保证实验成功:∠MOA____________,原因是____________________________________.