某商场预计从2013年1月份起的前x个月,顾客对某商品的需求总量p(x)(单位:件)与x的关系近似的满足 ,且
,且 )。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
)。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
(1)写出这种商品2013年第x月的需求量f(x)(单位:件)与x的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问该商场2013年第几个月销售该商品的月利润最大,最大月利润为多少元?
如图,在三棱柱ABC—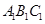 中,底面
中,底面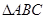 为正三角形,
为正三角形,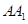
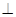 平面ABC,
平面ABC,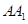 =2AB,N是
=2AB,N是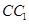 的中点,M是线段
的中点,M是线段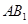 上的动点。
上的动点。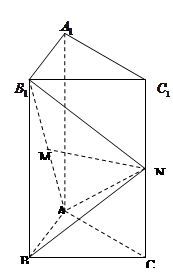
(1)当M在什么位置时,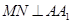 ,请给出证明;
,请给出证明;
(2)若直线MN与平面ABN所成角的大小为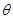 ,求
,求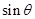 的最大值。
的最大值。
已知数列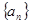 的前项和为
的前项和为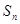 ,满足
,满足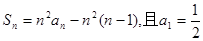 ,
,
(1)令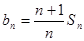 ,证明:
,证明: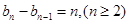 ;
;
(2)求数列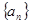 的通项公式。
的通项公式。
设对于任意实数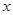 ,不等式
,不等式 恒成立.
恒成立.
(1)求 的取值范围;
的取值范围;
(2)当 取最大值时,解关于
取最大值时,解关于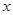 的不等式:
的不等式: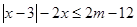 .
.
在平面直角坐标系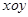 中,曲线
中,曲线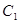 的参数方程为
的参数方程为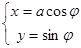 (
(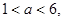
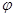 为参数),在以原点
为参数),在以原点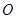 为极点,
为极点,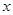 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线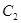 的极坐标方程为
的极坐标方程为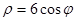 ,射线
,射线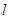 的方程为
的方程为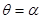 ,又
,又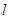 与
与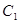 的交点为
的交点为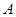 ,
,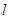 与
与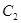 的除极点外的另一个交点为
的除极点外的另一个交点为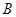 ,当
,当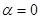 时,
时,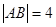 .
.
(1)求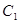 的普通方程,
的普通方程,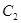 的直角坐标方程;
的直角坐标方程;
(2)设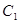 与
与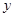 轴正半轴的交点为
轴正半轴的交点为 ,当
,当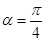 时,求直线
时,求直线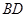 的参数方程.
的参数方程.
如图,四边形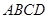 是☉
是☉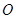 的内接四边形,
的内接四边形, 不经过点
不经过点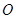 ,
,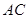 平分
平分 ,经过点
,经过点 的直线分别交
的直线分别交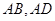 的延长线于点
的延长线于点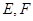 ,且
,且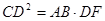 ,证明:
,证明: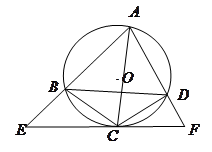
(1)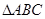 ∽
∽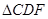 ;
;
(2)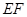 是☉
是☉ 的切线.
的切线.