已知函数 (
( ).
).
(Ⅰ)若函数 在定义域内单调递增,求实数
在定义域内单调递增,求实数 的取值范围;
的取值范围;
(Ⅱ)若 ,且关于
,且关于 的方程
的方程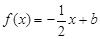 在
在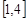 上恰有两个不等的实根,求实数
上恰有两个不等的实根,求实数 的取值范围;
的取值范围;
(Ⅲ)设各项为正数的数列 满足
满足 ,
, (
(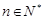 ),求证:
),求证: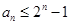 .
.
设函数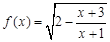 的定义域为A,不等式
的定义域为A,不等式 的解集为B.
的解集为B.
(1)求A;
(2)若B A,求实数a的取值范围
A,求实数a的取值范围
已知函数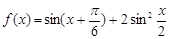 .
.
(1)求函数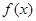 的单调递增区间;
的单调递增区间;
(2)记△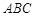 的内角
的内角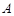 、
、 、
、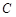 所对的边长分别为
所对的边长分别为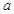 、
、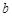 、
、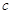 ,若
,若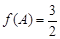 ,△
,△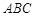 的面积
的面积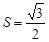 ,
,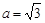 ,求
,求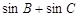 的值.
的值.
已知圆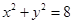 内有一点
内有一点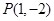 ,
, 为过点
为过点 且倾斜角为
且倾斜角为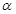 的弦,
的弦,
(1)当 时,求弦
时,求弦 的长.
的长.
(2)当弦 被点
被点 平分时,求出弦
平分时,求出弦 所在直线的方程.
所在直线的方程.
设 为关于n的k
为关于n的k 次多项式.数列{an}的首项
次多项式.数列{an}的首项 ,前n项和为
,前n项和为 .对于任意的正整数n,
.对于任意的正整数n, 都成立.
都成立.
(1)若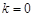 ,求证:数列{an}是等比数列;
,求证:数列{an}是等比数列;
(2)试确定所有的自然数k,使得数列{an}能成等差数列
若函数 为定义域
为定义域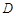 上单调函数,且存在区间
上单调函数,且存在区间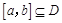 (其中
(其中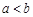 ),使得当
),使得当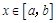 时,
时, 的取值范围恰为
的取值范围恰为 ,则称函数
,则称函数 是
是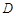 上的正函数,区间
上的正函数,区间 叫做等域区间.
叫做等域区间.
(1)已知 是
是 上的正函数,求
上的正函数,求 的等域区间;
的等域区间;
(2)试探究是否存在实数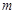 ,使得函数
,使得函数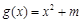 是
是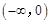 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数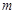 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.