(满分14分)设函数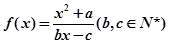 .若方程
.若方程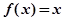 的根为0和2,且
的根为0和2,且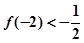 .
.
(1). 求函数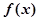 的解析式;
的解析式;
(2) 已知各项均不为零的数列 满足:
满足: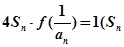 为该数列的前n项和),求该数列的通项
为该数列的前n项和),求该数列的通项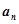 ;
;
(3)如果数列 满足
满足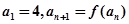 .求证:当
.求证:当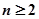 时,恒有
时,恒有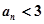 成立.
成立.
(满分14分)设函数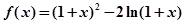 .
.
(1)求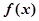 的单调区间;
的单调区间;
(2)若当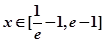 时,(其中
时,(其中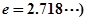 不等式
不等式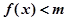 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)试讨论关于x的方程: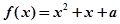 在区间[0,2]上的根的个数.
在区间[0,2]上的根的个数.
(满分14分)已知一动圆M,恒过点F(1,0),且总与直线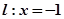 相切,
相切,
(Ⅰ)求动圆圆心M的轨迹C的方程;
(Ⅱ)在曲线C上是否存在异于原点的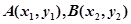 两点,当
两点,当 时,直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由.
时,直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由.
(满分14分)如图,在四面体ABCD中,O、E分别是BD、BC的中点,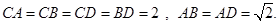

(Ⅰ)求证: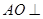 平面BCD;
平面BCD;
(Ⅱ)求异面直线AB与CD所成角的余弦值;
(Ⅲ)求点E到平面ACD的距离.
(满分12分)某次体能测试中,规定每名运动员一开始就要参加且最多参加四次测试.一旦测试通过,就不再参加余下的测试,否则一直参加完四次测试为止.已知运动员甲的每次通过率为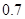 (假定每次通过率相同).
(假定每次通过率相同).
(1) 求运动员甲最多参加两次测试的概率;
(2) 求运动员甲参加测试的次数的分布列及数学期望(精确到0.1).