(满分12分)某次体能测试中,规定每名运动员一开始就要参加且最多参加四次测试.一旦测试通过,就不再参加余下的测试,否则一直参加完四次测试为止.已知运动员甲的每次通过率为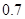 (假定每次通过率相同).
(假定每次通过率相同).
(1) 求运动员甲最多参加两次测试的概率;
(2) 求运动员甲参加测试的次数的分布列及数学期望(精确到0.1).
已知函数 .
.
(1)将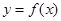 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数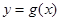 ,求
,求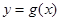 的解析式;
的解析式;
(2)函数 与函数
与函数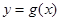 的图像关于直线
的图像关于直线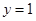 对称,求
对称,求 的解析式;
的解析式;
(3)设
 的最小值是
的最小值是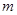 ,且
,且 ,求实数
,求实数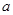 的取值范围.
的取值范围.
求函数 在
在 上的最大值,其中
上的最大值,其中
设函数f(x)=ax2+8x+3 a<0
a<0 。对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5恒成立.问:a为何值时,l(a)最大?求出这个最大的l(a),证明你的结论.
。对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5恒成立.问:a为何值时,l(a)最大?求出这个最大的l(a),证明你的结论.
设{a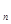 }是由正数组成的等比数列,S
}是由正数组成的等比数列,S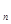 是前n项和。
是前n项和。
①证明: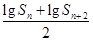 <lgS
<lgS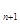 ;
;
②是否存在常数c>0,使得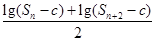 =lg(S
=lg(S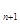 -c)成立?并证明结论。
-c)成立?并证明结论。
求证平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形.
已知:如图,三棱锥S—ABC,SC∥截面EFGH,AB∥截面EFGH.
求证:截面EFGH是平行四边形.