(满分14分)设函数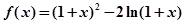 .
.
(1)求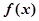 的单调区间;
的单调区间;
(2)若当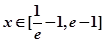 时,(其中
时,(其中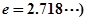 不等式
不等式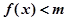 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)试讨论关于x的方程: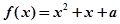 在区间[0,2]上的根的个数.
在区间[0,2]上的根的个数.
.(本小题满分13分)
已知D为 的边BC上一点,且
的边BC上一点,且
(1)求角A的大小;
(2)若 的面积为
的面积为 ,且
,且 ,求BD的长。
,求BD的长。
(本小题满分13分)
已知集合
(1)若 ,求m的值;
,求m的值;
(2)若 ,求m的取值范围。
,求m的取值范围。
.(本小题满分12分)
已知正项数列 满足:
满足:
(1)求 的范围,使得
的范围,使得 恒成立;
恒成立;
(2)若 ,证明
,证明
(3)若 ,证明:
,证明:
(本小题满分12分)
如题21图,已知离心率为 的椭圆
的椭圆 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。
(1)求椭圆C的方程。
(2)证明:直线MA、MB与x轴围成一个等腰三角形。
(本小题满分12分)
两非零向量 满足:
满足: 垂直,集合
垂直,集合 是单元素集合。
是单元素集合。
(1)求 的夹角;
的夹角;
(2)若关于t的不等式 的解集为空集,求实数m的值。
的解集为空集,求实数m的值。