已知数列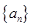 的前
的前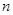 项和为
项和为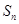 ,且满足:
,且满足: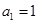 ,
,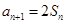 .
.
(1)求数列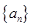 的通项公式;
的通项公式;
(2)设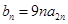 ,求数列
,求数列 的前
的前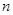 项和为
项和为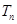 .
.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求 的概率.
的概率.
已知函数
(1)在给定的平面直角坐标系中,画函数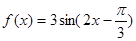 ,
, 的简图;
的简图;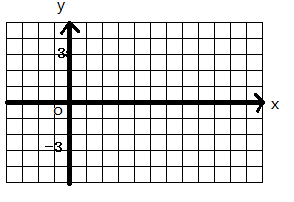
(2)求
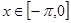 的单调增区间;
的单调增区间;
(3) 函数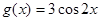 的图象只经过怎样的平移变换就可得到
的图象只经过怎样的平移变换就可得到 的图象?
的图象?
已知函数 的最大值为
的最大值为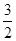 ,最小值为
,最小值为 .
.
(1)求 的值;
的值;
(2)已知函数 ,当
,当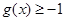 时求自变量x的集合.
时求自变量x的集合.
在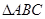 中,角
中,角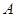 ,
, ,
,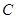 所对的边分别是
所对的边分别是 ,
, ,
, ,若
,若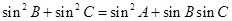 ,且
,且 ,求
,求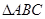 的面积
的面积 .
.
已知椭圆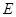 :
: 的离心率为
的离心率为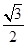 ,其长轴长与短轴长的和等于6.
,其长轴长与短轴长的和等于6.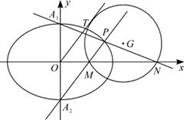
(1)求椭圆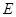 的方程;
的方程;
(2)如图,设椭圆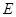 的上、下顶点分别为
的上、下顶点分别为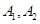 ,
,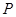 是椭圆上异于
是椭圆上异于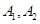 的任意一点,直线
的任意一点,直线 分别交
分别交 轴于点
轴于点 ,若直线
,若直线 与过点
与过点 的圆
的圆 相切,切点为
相切,切点为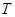 .证明:线段
.证明:线段 的长为定值.
的长为定值.