在△ABC中,角A,B,C所对的边分别为a,b,c,角A,B,C依次成等差数列.
(1)若sin2B-sinAsinC,试判断△ABC的形状;
(2)若△ABC为钝角三角形,且a>c,试求 的取值范围.
的取值范围.
(本小题满分12分)
已知函数f(x)="log" a  (a>0且a≠1)的图像关于原点对称
(a>0且a≠1)的图像关于原点对称
(1)求m的值;
(2)判断函数f(x)在区间(1,+∞)上的单调性并加以证明;
(3)当a>1,x∈(t,a)时, f(x)的值域是(1,+∞),求a与t的值。
(本小题满分12分)
在 中,角
中,角 所对的边分别为a,b,c.已知
所对的边分别为a,b,c.已知 且
且 .
.
(1)当 时,求
时,求 的值; (2)若角
的值; (2)若角 为锐角,求p的取值范围。
为锐角,求p的取值范围。
.(本小题满分12分) 如图,测量河对岸的塔高 时,可以选与塔底
时,可以选与塔底 在同一水平面内的两个侧点
在同一水平面内的两个侧点 与
与 .现测得
.现测得 ,并在点
,并在点 测得塔顶
测得塔顶 的仰角为
的仰角为 ,求塔高AB.
,求塔高AB.
(本小题满分12分)已知函数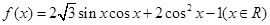
(Ⅰ)求函数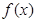 的最小正周期及在区间
的最小正周期及在区间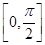 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若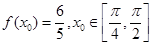 ,求
,求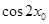 的值。
的值。