如图，矩形OABC的顶点B的坐标为(1，2)，反比例函数y＝
(0<m<2)的图象与AB交于点E，与BC交于点F，连接OE、OF、EF．
(1)若点E是AB的中点，则m＝ ，S△OEF＝ ；
(2)若S△OEF＝2S△BEF，求点E的坐标；
(3)是否存在点E及y轴上的点M，使得△MFE与△BFE全等?若存在，写出此时点E的坐标；若不存在，说明理由．
某学校为丰富大课间体育活动的内容，随机选取本校100名学生进行调查,调查内容是“你最喜欢的自由活动项目是什么?”，整理收集到的数据，绘制成如图所示的统计图．
（1）学校采用的调查方式是；
（2）写出喜欢“踢毽子”的学生人数，并在图中将“踢毽子”部分的图形补充完整；
（3）该校共有800名学生，请估计喜欢“跳绳”的学生人数．
如图，在ΔABC和ΔDCB中，AC与BD相交于点， AB = DC，AC = BD.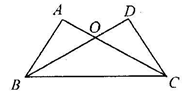
(1)求证: ΔABC≌ΔDCB；(2) Δ0BC的形状是(直接写出结论，不需证明) .
（1）解方程：
；
（2）解不等式组：
（1）计算： |－3|－(π－3)0+2sin30°；
（2）已知：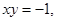
求代数式
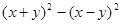的值．
如图，抛物线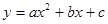
经过点A
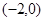、B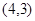
两点，且当x=3和x=-3时，这条抛物线上对应点的纵坐标相等，经过点C
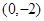的直线
与x轴平行．
（1）求这条抛物线的解析式；
（2）若D是直线上的一个动点，求使△DAB的周长最小时点D的坐标；
（3）以这条抛物线上的任意一点P为圆心，PO的长为半径作⊙P，试判断⊙P与直线的位置关系，并说明理由．