已知椭圆的中心为原点,焦点在 轴上,离心率为
轴上,离心率为 ,且经过点
,且经过点 ,直线
,直线 交椭圆于异于M的不同两点
交椭圆于异于M的不同两点 .直线
.直线 轴分别交于点
轴分别交于点 .
.
(1)求椭圆标准方程;
(2)求 的取值范围;
的取值范围;
(3)证明 是等腰三角形.
是等腰三角形.
若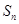 和
和 分别表示数列
分别表示数列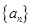 和数列
和数列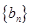 的前
的前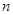 项和,对任意正整数
项和,对任意正整数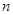 ,有
,有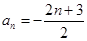 ,
,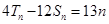 .
.
(1)求数列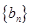 的通项公式;
的通项公式;
(2)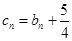 ,
,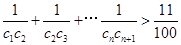 ,求
,求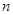 的最小值.
的最小值.
如图,四棱锥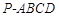 中,
中, ,
, 是矩形,
是矩形, 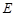 是棱
是棱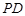 的中点,
的中点,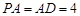 ,
,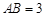 .
.
(1)证明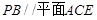 ;
;
(2)求直线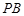 与平面
与平面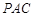 所成角的正弦值.
所成角的正弦值.
已知函数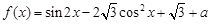 .
.
(1)求函数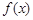 的单调递减区间;
的单调递减区间;
(2)设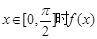 的最小值是
的最小值是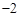 ,求
,求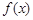 的最大值.
的最大值.
如图,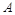 地在高压线
地在高压线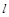 (不计高度)的东侧0.50km处,
(不计高度)的东侧0.50km处,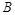 地在
地在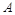 地东北方向1.00km处,公路沿线
地东北方向1.00km处,公路沿线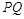 上任意一点到
上任意一点到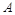 地与高压线
地与高压线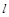 的距离相等.现要在公路旁建一配电房向
的距离相等.现要在公路旁建一配电房向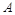 、
、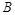 两地降压供电(分别向两地进线).经协商,架设低压线路部分的费用由
两地降压供电(分别向两地进线).经协商,架设低压线路部分的费用由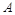 、
、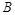 两地用户分摊, 为了使分摊费用总和最小,配电房应距高压线
两地用户分摊, 为了使分摊费用总和最小,配电房应距高压线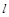
| A.1.21km | B.0.50km | C.0.75km | D.0.96km |