已知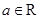 ,函数
,函数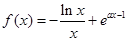 (
(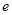 为自然对数的底数).
为自然对数的底数).
(Ⅰ)若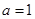 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅱ)若 的最小值为
的最小值为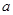 ,求
,求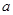 的最小值.
的最小值.
如图,在圆锥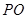 中,已知
中,已知 ,⊙O的直径
,⊙O的直径 ,
,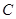 是
是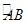 的中点,
的中点,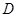 为
为 的中点.
的中点.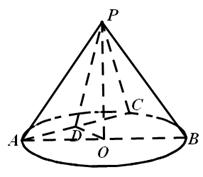
(1)证明:平面 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
甲、乙两位篮球运动员进行定点投篮,甲投篮一次命中的概率为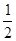 ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为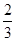 .每人各投4个球,两人投篮命中的概率互不影响.
.每人各投4个球,两人投篮命中的概率互不影响.
(1)求甲至多命中1个球且乙至少命中1个球的概率;
(2)若规定每投篮一次命中得3分,未命中得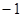 分,求乙所得分数
分,求乙所得分数 的概率分布和数学期望.
的概率分布和数学期望.
先后掷两颗均匀的骰子,问
(1)至少有一颗是6点的概率是多少?
(2)当第一颗骰子的点数为3或6时,求两颗骰子的点数之和大于8的概率.
已知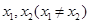 是函数
是函数 的两个极值点.
的两个极值点.
(1)若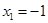 ,
,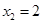 ,求函数
,求函数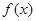 的解析式;
的解析式;
(2)若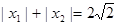 ,求实数
,求实数 的最大值;
的最大值;
(3)设函数 ,若
,若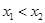 ,且
,且 ,求函数
,求函数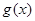 在
在 内的最小值.(用
内的最小值.(用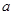 表示)
表示)
已知抛物线 的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴,垂足为T,与抛物线交于不同的两点P、Q且
的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴,垂足为T,与抛物线交于不同的两点P、Q且 .
.
(1)求点T的横坐标 ;
;
(2)若以F1,F2为焦点的椭圆C过点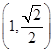 .
.
①求椭圆C的标准方程;
②过点F2作直线l与椭圆C交于A,B两点,求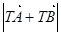 的取值范围.
的取值范围.