如图，在Rt△ABC中，∠ACB90°，AC8cm，AB10-优题课

如图，在Rt△ABC中，∠ACB=90°，AC=8cm，AB=10cm．点P从点A出发，以5cm/s的速度从点A运动到终点B；同时，点Q从点C出发，以3cm/s的速度从点C运动到终点B，连结PQ；过点P作PD⊥AC交AC于点D，将△APD沿PD翻折得到△A′PD，以A′P和PB为邻边作▱A′PBE，A′E交射线BC于点F，交射线PQ于点G．设▱A′PBE与四边形PDCQ重叠部分图形的面积为Scm²，点P的运动时间为ts．
（1）当t为何值时，点A′与点C重合；
（2）用含t的代数式表示QF的长；
（3）求S与t的函数关系式；
（4）请直接写出当射线PQ将▱A′PBE分成的两部分图形的面积之比是1：3时t的值．

科目数学题型解答题难度困难

知识点：二次函数在给定区间上的最值

已知函数 $y = x^{2} + bx + c (b$ ， $c$ 为常数）的图象经过点 $(- 2, 4)$ ．

（1）求 $b$ ， $c$ 满足的关系式；

（2）设该函数图象的顶点坐标是 $(m, n)$ ，当 $b$ 的值变化时，求 $n$ 关于 $m$ 的函数解析式；

（3）若该函数的图象不经过第三象限，当 $- 5 ⩽ x ⩽ 1$ 时，函数的最大值与最小值之差为16，求 $b$ 的值．

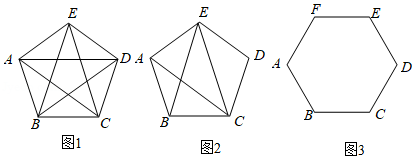
我们知道，各个角都相等，各条边都相等的多边形叫做正多边形．对一个各条边都相等的凸多边形（边数大于 $3)$ ，可以由若干条对角线相等判定它是正多边形．例如，各条边都相等的凸四边形，若两条对角线相等，则这个四边形是正方形．

（1）已知凸五边形 $ABCDE$ 的各条边都相等．

①如图1，若 $AC = AD = BE = BD = CE$ ，求证：五边形 $ABCDE$ 是正五边形；

②如图2，若 $AC = BE = CE$ ，请判断五边形 $ABCDE$ 是不是正五边形，并说明理由：

（2）判断下列命题的真假．（在括号内填写“真”或“假” $)$

如图3，已知凸六边形 $ABCDEF$ 的各条边都相等．

①若 $AC = CE = EA$ ，则六边形 $ABCDEF$ 是正六边形； $($ 　　 $)$

②若 $AD = BE = CF$ ，则六边形 $ABCDEF$ 是正六边形． $($ 　　 $)$

安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害，为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动．在活动前和活动后分别随机抽取了部分使用电瓶车的市民，就骑电瓶车戴安全帽情况进行问卷调查，将收集的数据制成如下统计图表．

（1）宣传活动前，在抽取的市民中哪一类别的人数最多？占抽取人数的百分之几？

（2）该市约有30万人使用电瓶车，请估计活动前全市骑电瓶车“都不戴”安全帽的总人数；

（3）小明认为，宣传活动后骑电瓶车“都不戴”安全帽的人数为178，比活动前增加了1人，因此交警部门开展的宣传活动没有效果．小明分析数据的方法是否合理？请结合统计图表，对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法．

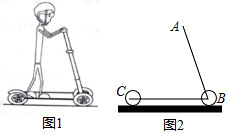
如图1，某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯．甲、乙两人从二楼同时下行，甲乘自动扶梯，乙走步行楼梯，甲离一楼地面的高度 $h$ （单位： $m)$ 与下行时间 $x$ （单位： $s)$ 之间具有函数关系 $h = - \frac{3}{10} x + 6$ ，乙离一楼地面的高度 $y$ （单位： $m)$ 与下行时间 $x$ （单位： $s)$ 的函数关系如图2所示．

（1）求 $y$ 关于 $x$ 的函数解析式；

（2）请通过计算说明甲、乙两人谁先到达一楼地面．

图1是一辆在平地上滑行的滑板车，图2是其示意图．已知车杆 $AB$ 长 $92 cm$ ，车杆与脚踏板所成的角 $∠ ABC = 70 °$ ，前后轮子的半径均为 $6 cm$ ，求把手 $A$ 离地面的高度（结果保留小数点后一位；参考数据： $\sin 70 ° \approx 0.94$ ， $\cos 70 ° \approx 0.34$ ， $\tan 70 ° \approx 2.75)$ ．