已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.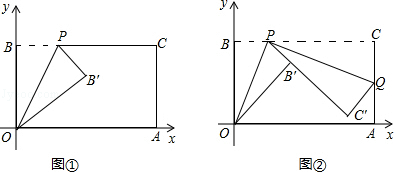
(Ⅰ)如图①,当∠BOP=30°时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;
(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).
、如图,一个直角三角形纸片的顶点A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.点A在移动的过程中,线段AD和AE有怎样的数量关系,并说明理由.
点A在移动的过程中,若射线ON上始终存在一点F与点A关于OP所在的直线对称,判断并说明以A、D、F、E为顶点的四边形是怎样特殊的四边形?
若∠MON=45°,猜想线段AC、AD、OC之间有怎样的数量关系,并证明你的猜想.

某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:
设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
(成本=进价×销售量)
小明家所在居民楼的对面有一座大厦AB,AB=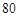 米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)(参考数据:
米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)(参考数据: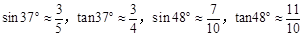 )
)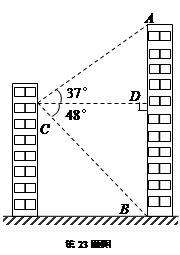
如图所示,AB是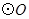 的直径,
的直径,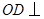 弦
弦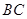 于点
于点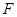 ,且交
,且交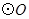 于点
于点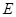 ,若
,若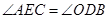 .
.判断直线
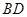 和
和 的位置关系,并给出证明;
的位置关系,并给出证明;当
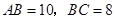 时,求
时,求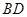 的长.
的长.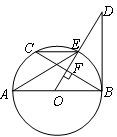
红星中学开展了“绿化家乡,植树造林 ”活动,并对该校的甲、乙、丙、丁四个班级种树情况进行了考察,并将收集的数据绘制了图①和图②两幅尚不完整的统计图.
请根据图中提供的信息,完成下列问题: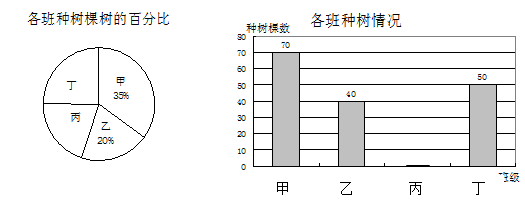
这四个班共种__▲______棵树.
请你补全两幅统计图.
若四个班种树的平均成活率是90%,全校共种树2000棵,请你估计这些树中,成活的树约有多少棵?