某市粮食储备库的设计容量为30万吨,年初库存粮食10万吨,从1月份起,计划每月收购粮食M万吨,每月供给市面粉厂粮食1万吨,另外每月还有大量的粮食外调任务。已知n个月内外调粮食的总量为 万吨与n的函数关系为
万吨与n的函数关系为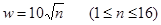 .要使在16个月内每月粮食收购之后能满足内、外调需要,且每月粮食调出后粮库内有不超过设计容量的储备粮,求M的范围。
.要使在16个月内每月粮食收购之后能满足内、外调需要,且每月粮食调出后粮库内有不超过设计容量的储备粮,求M的范围。
如图,在三棱柱 中,
中, ,顶点
,顶点 在底面
在底面 上的射影恰为点
上的射影恰为点 ,
, .
.
(1)证明:平面 平面
平面 ;
;
(2 )若点 为
为 的中点,求出二面角
的中点,求出二面角 的余弦值.
的余弦值.
(1)证明:平面 平面
平面 ;
;
(2)若点 为
为 的中点,求出二面角
的中点,求出二面角 的余弦值.
的余弦值.
已知数列{an}的各项均为正数的等比数列,且a1a2=2,a3a4=32,
(1)求数列{an}的通项公式;
(2)设数列{bn}满足 (n∈N*),求设数列{bn}的前n项和Tn.
(n∈N*),求设数列{bn}的前n项和Tn.
已知函数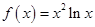 .
.
(1)求函数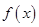 的单调区间;
的单调区间;
(2)证明:对任意的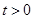 ,存在唯一的
,存在唯一的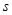 ,使
,使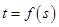 ;
;
(3)设(2)中所确定的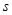 关于
关于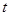 的函数为
的函数为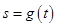 ,证明:当
,证明:当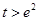 时,有
时,有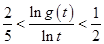 .
.
如图,点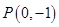 是椭圆
是椭圆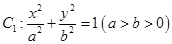 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆 的直径,
的直径,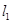 、
、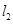 是过点
是过点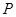 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中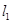 交圆
交圆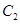 于
于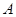 、
、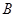 两点,
两点,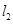 交椭圆
交椭圆 于另一点
于另一点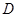 .
.
(1)求椭圆 的方程;
的方程;
(2)求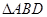 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线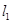 的方程.
的方程.
已知等差数列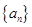 的首项
的首项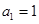 ,公差
,公差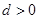 ,且
,且 、
、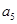 、
、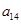 分别是等比数列
分别是等比数列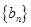 的
的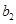 、
、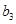 、
、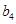 .
.
(1)求数列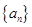 和
和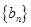 的通项公式;
的通项公式;
(2)设数列 对任意正整数
对任意正整数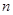 均有
均有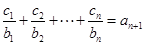 成立,求
成立,求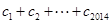 的值.
的值.